Difference between revisions of "Lebesgue constants"
(→References: Finch (2003)) |
m (→References: link) |
||
| Line 41: | Line 41: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969) pp. Sect. 4.2</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969) pp. Sect. 4.2</TD></TR></table> | ||
| + | |||
| + | ====Comments==== | ||
The Lebesgue constants of an interpolation process are the numbers | The Lebesgue constants of an interpolation process are the numbers | ||
| Line 52: | Line 54: | ||
and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780029.png" /> are pairwise distinct interpolation points lying in some interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780030.png" />. | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780029.png" /> are pairwise distinct interpolation points lying in some interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780030.png" />. | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780032.png" /> be, respectively, the space of continuous functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780033.png" /> and the space of algebraic polynomials of degree at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780034.png" />, considered on the same interval, with the uniform metric, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780035.png" /> be the interpolation polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780036.png" /> that takes the same values at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780038.png" />, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780039.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780040.png" /> denotes the operator that associates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780041.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780042.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780043.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780044.png" />, where the left-hand side is the operator norm in the space of bounded linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780045.png" /> and | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780032.png" /> be, respectively, the space of continuous functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780033.png" /> and the space of algebraic polynomials of degree at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780034.png" />, considered on the same interval, with the uniform metric, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780035.png" /> be the interpolation polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780036.png" /> that takes the same values at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780038.png" />, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780039.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780040.png" /> denotes the operator that associates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780041.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780042.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780043.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780044.png" />, where the left-hand side is the [[operator norm]] in the space of bounded linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780045.png" /> and |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780046.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057800/l05780046.png" /></td> </tr></table> | ||
Revision as of 17:10, 29 October 2017
The quantities
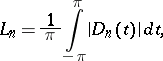 |
where
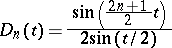 |
is the Dirichlet kernel. The Lebesgue constants 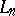 for each
for each  equal:
equal:
1) the maximum value of  for all
for all  and all continuous functions
and all continuous functions 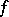 such that
such that 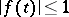 for almost-all
for almost-all 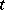 ;
;
2) the least upper bound of 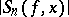 for all
for all  and all continuous functions
and all continuous functions 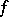 such that
such that 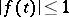 ;
;
3) the least upper bound of the integrals
 |
for all functions 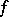 such that
such that
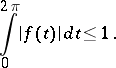 |
Here 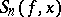 is the
is the  -th partial sum of the trigonometric Fourier series of the
-th partial sum of the trigonometric Fourier series of the 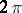 -periodic function
-periodic function 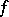 . The following asymptotic formula is valid:
. The following asymptotic formula is valid:
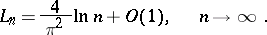 |
In particular, 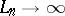 as
as 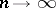 ; this is connected with the divergence of the trigonometric Fourier series of certain continuous functions. In a wider sense the Lebesgue constants are defined for other orthonormal systems (cf. Orthogonal system) as the quantities
; this is connected with the divergence of the trigonometric Fourier series of certain continuous functions. In a wider sense the Lebesgue constants are defined for other orthonormal systems (cf. Orthogonal system) as the quantities
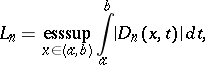 |
where  is the Dirichlet kernel for the given orthonormal system of functions on
is the Dirichlet kernel for the given orthonormal system of functions on 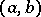 ; they play an important role in questions of convergence of Fourier series in these systems. The Lebesgue constants were introduced by H. Lebesgue (1909). See also Lebesgue function.
; they play an important role in questions of convergence of Fourier series in these systems. The Lebesgue constants were introduced by H. Lebesgue (1909). See also Lebesgue function.
References
| [1] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
Comments
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6 |
| [a2] | T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969) pp. Sect. 4.2 |
Comments
The Lebesgue constants of an interpolation process are the numbers
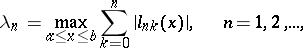 |
where
 |
and  are pairwise distinct interpolation points lying in some interval
are pairwise distinct interpolation points lying in some interval 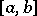 .
.
Let 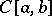 and
and 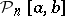 be, respectively, the space of continuous functions on
be, respectively, the space of continuous functions on 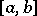 and the space of algebraic polynomials of degree at most
and the space of algebraic polynomials of degree at most  , considered on the same interval, with the uniform metric, and let
, considered on the same interval, with the uniform metric, and let 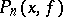 be the interpolation polynomial of degree
be the interpolation polynomial of degree 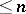 that takes the same values at the points
that takes the same values at the points 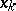 ,
, 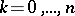 , as
, as 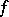 . If
. If 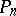 denotes the operator that associates
denotes the operator that associates 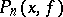 with
with 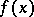 , i.e.
, i.e. 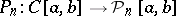 , then
, then  , where the left-hand side is the operator norm in the space of bounded linear operators
, where the left-hand side is the operator norm in the space of bounded linear operators 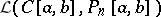 and
and
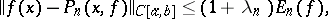 |
where  is the best approximation of
is the best approximation of 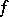 by algebraic polynomials of degree at most
by algebraic polynomials of degree at most  .
.
For any choice of the interpolation points in 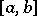 , one has
, one has 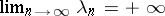 . For equidistant points a constant
. For equidistant points a constant 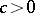 exists such that
exists such that 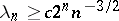 . In case of the interval
. In case of the interval  , for points coinciding with the zeros of the
, for points coinciding with the zeros of the  -th Chebyshev polynomial, the Lebesgue constants have minimum order of growth, namely
-th Chebyshev polynomial, the Lebesgue constants have minimum order of growth, namely
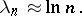 |
If 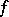 is
is 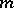 times differentiable on
times differentiable on 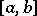 ,
, 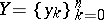 is a given set of numbers ( "approximations of the values fxk" ),
is a given set of numbers ( "approximations of the values fxk" ), 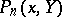 is the interpolation polynomial of degree
is the interpolation polynomial of degree 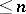 that takes the values
that takes the values 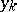 at the points
at the points 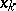 ,
, 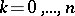 , and
, and
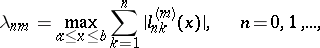 |
then
 |
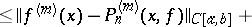 |
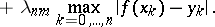 |
The Lebesgue constants 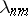 of an arbitrary interval
of an arbitrary interval 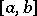 are connected with the analogous constants
are connected with the analogous constants  for the interval
for the interval 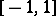 by the relation
by the relation
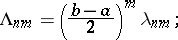 |
in particular, 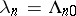 .
.
L.D. Kudryavtsev
Comments
The problem to determine "optimal nodes" , i.e., for  a fixed positive integer
a fixed positive integer 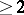 , to determine
, to determine  such that
such that 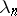 is minimal, has been given much attention. S.N. Bernstein [S.N. Bernshtein] (1931) conjectured that
is minimal, has been given much attention. S.N. Bernstein [S.N. Bernshtein] (1931) conjectured that 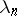 is minimal when
is minimal when 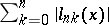 "equi-oscillates" . Bernstein's conjecture was proved by T.A. Kilgore (cf. [a1]); historical notes are also included there.
"equi-oscillates" . Bernstein's conjecture was proved by T.A. Kilgore (cf. [a1]); historical notes are also included there.
References
| [a1] | T.A. Kilgore, "A characterization of the Lagrange interpolation projection with minimal Tchebycheff norm" J. Approx. Theory , 24 (1978) pp. 273–288 |
| [a2] | T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969) pp. Sect. 4.2 |
| [a3] | Steven R. Finch, Mathematical Constants, Cambridge University Press (2003) ISBN 0-521-81805-2. Sect. 4.2 |
Lebesgue constants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_constants&oldid=42218