Difference between revisions of "Height, in Diophantine geometry"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A certain numerical function on the set of solutions of a Diophantine equation (cf. [[ | + | A certain numerical function on the set of solutions of a Diophantine equation (cf. [[Diophantine equations]]). In the simplest case of a solution in integers $(x_0,\ldots,x_n)$ of a Diophantine equation, the height is a function of the solution, and equals $\max\{|x_i|\}$. It is encountered in this form in Fermat's method of descent. Let $X$ be a projective algebraic variety defined over a [[global field]] $K$. The height is a class of real-valued functions $h_L(P)$ defined on the set $X(K)$ of rational points $P$ and depending on a morphism $L:X\rightarrow P^n$ of the variety $X$ into the projective space $P^n$. Each function in this class is also called a height. From the point of view of estimating the number of rational points there are no essential differences between the functions in this class: for any two functions $h'$ and $h''$ there exist constants $c',c'' > 0$, such that $c' h' \le h'' \le c''h'$. Such functions are called equivalent, and this equivalence is denoted (here) as $\cong$. |
| − | Fundamental properties of the height. The function | + | Fundamental properties of the height. The function $h_L(P)$ is functorial with respect to $P$, i.e. for any morphism $f:X \rightarrow Y$ and morphism $L : Y \rightarrow P^n$, |
| + | $$ | ||
| + | h_{f*L}(P) \cong h_L(f(P))\,\ \ P \in X(K) \ . | ||
| + | $$ | ||
| − | + | If the morphisms $L$, $L_1$ and $L_2$ are defined by invertible sheaves $\mathcal{L}$, $\mathcal{L}_1$ and $\mathcal{L}_2$, and if $\mathcal{L} = \mathcal{L}_1 \otimes \mathcal{L}_2$, then $h_L \cong h_{L_1} h_{L_2}$. The set of points $P \in X(K)$ of bounded height is finite in the following sense: If the basic field $K$ is an [[algebraic number field]], the set is finite; if it is an algebraic function field with field of constants $k$, the elements of $X(K)$ depend on a finite number of parameters from the field $k$; in particular, $X(K)$ is finite if the field $k$ is finite. Let $|\cdot|_\nu$ run through the set of all norms of $K$. One may then define the height of a point $(x_0:\cdots:x_n)$ of the projective space $P^n$ with coordinates from $K$ as | |
| − | |||
| − | If the morphisms | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h046/h046810/h04681042.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h046/h046810/h04681042.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | ||
| Line 14: | Line 15: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Weil, "Number theory and algebraic geometry" , ''Proc. Internat. Congress Mathematicians (Cambridge, 1950)'' , '''2''' , Amer. Math. Soc. (1952) pp. 90–100 {{MR|0045416}} {{ZBL|0049.02802}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Diophantine geometry" , Interscience (1962) {{MR|0142550}} {{ZBL|0115.38701}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) (Appendix in Russian translation: Yu.I. Manin; The Mordell–Weil theorem (in Russian)) {{MR|2514037}} {{MR|1083353}} {{MR|0352106}} {{MR|0441983}} {{MR|0282985}} {{MR|0248146}} {{MR|0219542}} {{MR|0219541}} {{MR|0206003}} {{MR|0204427}} {{ZBL|0326.14012}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.I. Manin, "Height of theta points on an Abelian manifold, their variants and applications" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''28''' (1964) pp. 1363–1390 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Mumford, "A remark on Mordell's conjecture" ''Amer. J. Math.'' , '''87''' (1965) pp. 1007–1016 {{MR|186624}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Néron, "Quasi-fonctions et hauteurs sur les variétés abéliennes" ''Ann. of Math. (2)'' , '''82''' (1965) pp. 249–331 {{MR|0179173}} {{ZBL|0163.15205}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> A. Weil, "Number theory and algebraic geometry" , ''Proc. Internat. Congress Mathematicians (Cambridge, 1950)'' , '''2''' , Amer. Math. Soc. (1952) pp. 90–100 {{MR|0045416}} {{ZBL|0049.02802}} </TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Diophantine geometry" , Interscience (1962) {{MR|0142550}} {{ZBL|0115.38701}} </TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) (Appendix in Russian translation: Yu.I. Manin; The Mordell–Weil theorem (in Russian)) {{MR|2514037}} {{MR|1083353}} {{MR|0352106}} {{MR|0441983}} {{MR|0282985}} {{MR|0248146}} {{MR|0219542}} {{MR|0219541}} {{MR|0206003}} {{MR|0204427}} {{ZBL|0326.14012}} </TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.I. Manin, "Height of theta points on an Abelian manifold, their variants and applications" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''28''' (1964) pp. 1363–1390 (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> D. Mumford, "A remark on Mordell's conjecture" ''Amer. J. Math.'' , '''87''' (1965) pp. 1007–1016 {{MR|186624}} {{ZBL|}} </TD></TR> | ||
| + | <TR><TD valign="top">[6]</TD> <TD valign="top"> A. Néron, "Quasi-fonctions et hauteurs sur les variétés abéliennes" ''Ann. of Math. (2)'' , '''82''' (1965) pp. 249–331 {{MR|0179173}} {{ZBL|0163.15205}} </TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | The notion of height is a major tool in arithmetic algebraic geometry. It plays an important role in Faltings' proof of the Tate conjecture on endomorphisms of Abelian varieties over number fields, the Shafarevich conjecture that there are only finitely many isomorphism classes of Abelian varieties over a number field over | + | The notion of height is a major tool in arithmetic algebraic geometry. It plays an important role in Faltings' proof of the Tate conjecture on endomorphisms of Abelian varieties over number fields, the Shafarevich conjecture that there are only finitely many isomorphism classes of Abelian varieties over a number field over $K$ of given dimension $g\ge1$ with good reduction outside a finite set of places $S$ of $K$, and the Mordell conjecture on the finiteness of the set of rational points $X(K)$ of a smooth curve of genus $g \ge 2$ over a number field $K$. Heights also play an important role in Arakelov intersection theory, which via moduli spaces of algebraic curves has also become important in string theory in mathematical physics. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Faltings (ed.) G. Wüstholtz (ed.) , ''Rational points'' , Vieweg (1986) {{MR|0863887}} {{ZBL|0636.14019}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Faltings (ed.) G. Wüstholtz (ed.) , ''Rational points'' , Vieweg (1986) {{MR|0863887}} {{ZBL|0636.14019}} </TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 11:50, 29 October 2017
A certain numerical function on the set of solutions of a Diophantine equation (cf. Diophantine equations). In the simplest case of a solution in integers $(x_0,\ldots,x_n)$ of a Diophantine equation, the height is a function of the solution, and equals $\max\{|x_i|\}$. It is encountered in this form in Fermat's method of descent. Let $X$ be a projective algebraic variety defined over a global field $K$. The height is a class of real-valued functions $h_L(P)$ defined on the set $X(K)$ of rational points $P$ and depending on a morphism $L:X\rightarrow P^n$ of the variety $X$ into the projective space $P^n$. Each function in this class is also called a height. From the point of view of estimating the number of rational points there are no essential differences between the functions in this class: for any two functions $h'$ and $h''$ there exist constants $c',c'' > 0$, such that $c' h' \le h'' \le c''h'$. Such functions are called equivalent, and this equivalence is denoted (here) as $\cong$.
Fundamental properties of the height. The function $h_L(P)$ is functorial with respect to $P$, i.e. for any morphism $f:X \rightarrow Y$ and morphism $L : Y \rightarrow P^n$, $$ h_{f*L}(P) \cong h_L(f(P))\,\ \ P \in X(K) \ . $$
If the morphisms $L$, $L_1$ and $L_2$ are defined by invertible sheaves $\mathcal{L}$, $\mathcal{L}_1$ and $\mathcal{L}_2$, and if $\mathcal{L} = \mathcal{L}_1 \otimes \mathcal{L}_2$, then $h_L \cong h_{L_1} h_{L_2}$. The set of points $P \in X(K)$ of bounded height is finite in the following sense: If the basic field $K$ is an algebraic number field, the set is finite; if it is an algebraic function field with field of constants $k$, the elements of $X(K)$ depend on a finite number of parameters from the field $k$; in particular, $X(K)$ is finite if the field $k$ is finite. Let $|\cdot|_\nu$ run through the set of all norms of $K$. One may then define the height of a point $(x_0:\cdots:x_n)$ of the projective space $P^n$ with coordinates from $K$ as
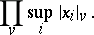 | (*) |
This is well defined because of the product formula 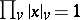 ,
,  . Let
. Let 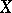 be an arbitrary projective variety over
be an arbitrary projective variety over 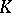 and let
and let 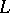 be a closed imbedding of
be a closed imbedding of 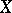 into the projective space; the height
into the projective space; the height 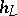 may then be obtained by transferring the function (*), using the imbedding, to the set
may then be obtained by transferring the function (*), using the imbedding, to the set 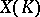 . Various projective imbeddings, corresponding to the same sheaf
. Various projective imbeddings, corresponding to the same sheaf 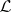 , define equivalent functions on
, define equivalent functions on 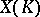 . A linear extension yields the desired function
. A linear extension yields the desired function 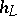 . The function
. The function  is occasionally replaced by its logarithm — the so-called logarithmic height.
is occasionally replaced by its logarithm — the so-called logarithmic height.
The above estimates may sometimes follow from exact equations [3], [4], [5]. There is a variant of the height function — the Néron–Tate height — which is defined on Abelian varieties and behaves as a functor with respect to the morphisms of Abelian varieties preserving the zero point. For the local aspect see [6]. The local components of a height constructed there play the role of intersection indices in arithmetic.
References
| [1] | A. Weil, "Number theory and algebraic geometry" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 2 , Amer. Math. Soc. (1952) pp. 90–100 MR0045416 Zbl 0049.02802 |
| [2] | S. Lang, "Diophantine geometry" , Interscience (1962) MR0142550 Zbl 0115.38701 |
| [3] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) (Appendix in Russian translation: Yu.I. Manin; The Mordell–Weil theorem (in Russian)) MR2514037 MR1083353 MR0352106 MR0441983 MR0282985 MR0248146 MR0219542 MR0219541 MR0206003 MR0204427 Zbl 0326.14012 |
| [4] | Yu.I. Manin, "Height of theta points on an Abelian manifold, their variants and applications" Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 1363–1390 (In Russian) |
| [5] | D. Mumford, "A remark on Mordell's conjecture" Amer. J. Math. , 87 (1965) pp. 1007–1016 MR186624 |
| [6] | A. Néron, "Quasi-fonctions et hauteurs sur les variétés abéliennes" Ann. of Math. (2) , 82 (1965) pp. 249–331 MR0179173 Zbl 0163.15205 |
Comments
The notion of height is a major tool in arithmetic algebraic geometry. It plays an important role in Faltings' proof of the Tate conjecture on endomorphisms of Abelian varieties over number fields, the Shafarevich conjecture that there are only finitely many isomorphism classes of Abelian varieties over a number field over $K$ of given dimension $g\ge1$ with good reduction outside a finite set of places $S$ of $K$, and the Mordell conjecture on the finiteness of the set of rational points $X(K)$ of a smooth curve of genus $g \ge 2$ over a number field $K$. Heights also play an important role in Arakelov intersection theory, which via moduli spaces of algebraic curves has also become important in string theory in mathematical physics.
References
| [a1] | G. Faltings (ed.) G. Wüstholtz (ed.) , Rational points , Vieweg (1986) MR0863887 Zbl 0636.14019 |
Height, in Diophantine geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Height,_in_Diophantine_geometry&oldid=42211