Difference between revisions of "Rational variety"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (link) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766010.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766010.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766011.png" /> is the canonical divisor of the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766012.png" />, that is, the [[Kodaira dimension|Kodaira dimension]] of the rational variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766013.png" /> is equal to 0. | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766011.png" /> is the [[canonical divisor]] of the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766012.png" />, that is, the [[Kodaira dimension|Kodaira dimension]] of the rational variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766013.png" /> is equal to 0. |
In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766014.png" /> and the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766015.png" /> is equal to 0, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766016.png" /> is a [[Rational curve|rational curve]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766017.png" />, the arithmetic genus | In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766014.png" /> and the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766015.png" /> is equal to 0, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766016.png" /> is a [[Rational curve|rational curve]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766017.png" />, the arithmetic genus | ||
Revision as of 18:22, 19 October 2017
An algebraic variety 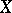 , defined over an algebraically closed field
, defined over an algebraically closed field 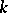 , whose field of rational functions
, whose field of rational functions 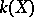 is isomorphic to a purely transcendental extension of
is isomorphic to a purely transcendental extension of 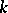 of finite degree. In other words, a rational variety is an algebraic variety
of finite degree. In other words, a rational variety is an algebraic variety 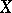 that is birationally isomorphic to a projective space
that is birationally isomorphic to a projective space  .
.
A complete smooth rational variety possesses the following birational invariants. The dimensions of all spaces  of regular differential
of regular differential 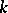 -forms on
-forms on  are equal to 0. In addition, the multiple genus
are equal to 0. In addition, the multiple genus
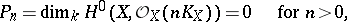 |
where 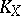 is the canonical divisor of the algebraic variety
is the canonical divisor of the algebraic variety 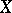 , that is, the Kodaira dimension of the rational variety
, that is, the Kodaira dimension of the rational variety  is equal to 0.
is equal to 0.
In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if 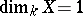 and the genus of
and the genus of 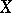 is equal to 0, then
is equal to 0, then  is a rational curve. If
is a rational curve. If 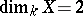 , the arithmetic genus
, the arithmetic genus
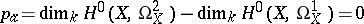 |
and the multiple genus 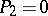 , then
, then 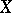 is a rational surface. However, if
is a rational surface. However, if 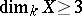 , there is no good criterion of rationality, due to the negative solution of the Lüroth problem.
, there is no good criterion of rationality, due to the negative solution of the Lüroth problem.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Comments
References
| [a1] | A. Beauville, J.-L. Colliot-Hélène, J.J. Sansuc, P. Swinnerton-Dyer, "Variétés stablement rationelles non-rationelles" Ann. of Math. , 121 (1985) pp. 283–318 |
Rational variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_variety&oldid=42127