Difference between revisions of "Computable function"
(Importing text file) |
(→Partial recursive functions.: TeX done) |
||
| Line 27: | Line 27: | ||
==Partial recursive functions.== | ==Partial recursive functions.== | ||
| − | All known examples of algorithms may be reduced to the problem of computing the values of a suitable function. Taking this feature as the fundamental property, Church, Gödel and Kleene defined a wide class of functions, which they named partial recursive. Let | + | All known examples of algorithms may be reduced to the problem of computing the values of a suitable function. Taking this feature as the fundamental property, Church, Gödel and Kleene defined a wide class of functions, which they named partial recursive. Let $F$ be the class of partial functions, with domains of definition and ranges of values in the set of natural numbers. The following operations are defined on the set $F$: |
| − | a) superposition (composition) of functions: If | + | a) superposition (composition) of functions: If $f,\alpha_1,\ldots,a_m \in F$, then one says that the function |
| + | $$ | ||
| + | \phi(x_1,\ldots,x_n) = f(\alpha_1(x_1,\ldots,x_n),\ldots,\alpha_m(x_1,\ldots,x_n)) | ||
| + | $$ | ||
| + | is obtained from $f,\alpha_1,\ldots,a_m$ by composition; | ||
| − | + | b) the $\mu$ or [[least-number operator]]: Let $f_1,f_2 \in F$; one says that a function $\psi$ is obtained from $f_1$ and $f_2$ with the aid of the $\mu$-operator, written as | |
| + | $$ | ||
| + | \psi(x_1,\ldots,x_n) = \mu y [f_1,f_2,(x_1,\ldots,x_n),y] | ||
| + | $$ | ||
| + | if $f_1(x_1,\ldots,x_n,z)$ and $f_2(x_1,\ldots,x_n,z)$ are defined and are unequal for $z<y$ and if | ||
| + | $$ | ||
| + | f_1(x_1,\ldots,x_n,y) = f_2(x_1,\ldots,x_n,y) | ||
| + | $$ | ||
| + | and then | ||
| + | $$ | ||
| + | \psi(x_1,\ldots,x_n) = y \ . | ||
| + | $$ | ||
| − | + | Clearly, if these operations are applied to functions the values of which one can compute, then there exist algorithms for computing the values of the functions $\phi$ and $\psi$. The following functions are considered to be the simplest: ${+},{\times}$, $\mathrm{pr}_i : ( x_1,\ldots,x_n) \mapsto x_i$, and | |
| − | + | $$ | |
| − | + | k(x,y) = \begin{cases} 1 & \ \text{if}\ x < y \\ 0 & \ \text{otherwise} \end{cases} \ . | |
| − | + | $$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Clearly, if these operations are applied to functions the values of which one can compute, then there exist algorithms for computing the values of the functions | ||
| − | |||
| − | |||
There exist easy algorithms which serve to compute the values of the simplest functions. | There exist easy algorithms which serve to compute the values of the simplest functions. | ||
| − | A function | + | A function $f$ is called partial recursive if it can be obtained by a finite number of steps from the simplest functions using the composition and the $\mu$-operator. A partial recursive function which is everywhere defined is called general recursive. The value of any partial recursive function may be effectively computed in the intuitive sense. The converse of this statement is known as Church's thesis: Any function the value of which can be effectively computed is partial recursive. Thus, according to Church's thesis, computable functions are partial recursive. |
==The normal algorithms of Markov.== | ==The normal algorithms of Markov.== | ||
Latest revision as of 19:56, 5 September 2017
A function the values of which may be computed with the aid of an effective procedure which is given in advance or by an algorithm. The characteristic feature of computational processes is the fact that the unknown quantities of the problem are successively computed from the given initial values by definite, pre-determined rules and instructions. The numerous available examples of computational processes in mathematics gave rise to an intuitive concept of a computational procedure. In the context of the general program for the foundation of mathematics, embarked upon in the 20th century, the need arose for an exact, as distinct from an intuitive, notion of algorithm. Exact definitions of computable functions, effective procedures and algorithms were given in various forms by D. Hilbert, K. Gödel, A. Church, S.C. Kleene, E.L. Post, A.M. Turing, and A.A. Markov.
The general idea underlying the different approaches to the establishment of rigorous mathematical definitions may be stated as follows. A detailed analysis is conducted of computational processes which are already known or which are conceivable, the important characteristics of these processes are revealed, and suitable mathematical analogues are found of these processes and their characteristic features. The realization of the different aspects of this idea is not unambiguous and results in different versions of the mathematical concept of an algorithm. The basic mathematical models of the concept of an algorithm are Turing machines, partial recursive functions, the normal algorithms of Markov, and others.
Turing machines.
Algorithms used in mathematics resemble machines working on separate lines which respond after a finite number of lines. Turing and Post described the concepts of abstract computers (cf. Computer, abstract) on which the computational processes may be modelled. A Turing machine (or a Turing–Post machine) 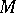 consists of:
consists of:
a) a finite alphabet 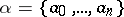 , where
, where  are arbitrary symbols; finite ordered sequence of symbols of the alphabet
are arbitrary symbols; finite ordered sequence of symbols of the alphabet 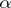 are called words over the alphabet
are called words over the alphabet 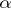 ; the words over the alphabet
; the words over the alphabet 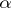 serve to encode the initial problems, the intermediate computations and the answers obtained;
serve to encode the initial problems, the intermediate computations and the answers obtained;
b) a finite list 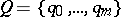 of elementary states which can be assumed by machine
of elementary states which can be assumed by machine 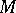 ;
; 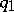 is considered to be the initial state of
is considered to be the initial state of 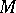 when it begins working, while
when it begins working, while 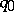 is the final state: If
is the final state: If 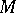 is brought to state
is brought to state 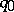 , it ceases operating;
, it ceases operating;
c) programs, consisting of individual commands 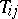 which have one of the forms
which have one of the forms 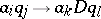 , where
, where 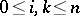 ,
, 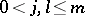 , and
, and 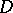 is one of the symbols of motion —
is one of the symbols of motion — 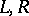 or
or 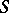 .
.
The configuration of the machine 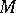 at a given moment of time is encoded by a word of the form
at a given moment of time is encoded by a word of the form 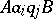 , where
, where 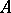 and
and 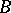 are certain words over the alphabet
are certain words over the alphabet 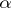 (the empty word
(the empty word 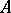 is written as
is written as 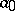 ). The configuration of the machine
). The configuration of the machine 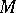 at a subsequent moment of time (after the completion of one time of work) is also coded by the word depending on the command
at a subsequent moment of time (after the completion of one time of work) is also coded by the word depending on the command 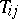 :
:
if  , the word obtained is
, the word obtained is 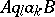 ;
;
if 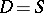 , the word obtained is
, the word obtained is 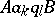 ;
;
if 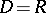 and
and 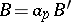 , the word obtained is
, the word obtained is 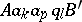 ;
;
if 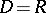 and
and 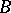 is the empty word, the word obtained is
is the empty word, the word obtained is 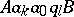 .
.
The mode of operation of the machine 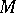 may be described as follows. The inputs are coded with the aid of some initial configuration (here
may be described as follows. The inputs are coded with the aid of some initial configuration (here  ); in accordance with the program of
); in accordance with the program of 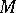 the following configuration is obtained, etc.; if at a certain moment the configuration obtained contains the final state
the following configuration is obtained, etc.; if at a certain moment the configuration obtained contains the final state 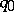 , the computation ends; the final configuration is decoded and constitutes the answer; if the machine never stops, the answer to the problem is considered to be indefinite.
, the computation ends; the final configuration is decoded and constitutes the answer; if the machine never stops, the answer to the problem is considered to be indefinite.
Any computational procedure which may be reduced to the operation of a suitable Turing machine is intuitively effective. The converse of this proposition is the so-called Turing thesis: Any effective computational procedure can be realized on an appropriate machine 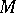 . This thesis cannot be demonstrated, since it contains two concepts — the rigorous mathematical definition of a Turing machine and the vague, intuitive concept of an effective procedure. If the Turing machines are made to model the computation of the values of a function whose domain of definition and whose range are sets of natural numbers, then one arrives at the concept of a computable function (on a Turing machine). See also Turing machine.
. This thesis cannot be demonstrated, since it contains two concepts — the rigorous mathematical definition of a Turing machine and the vague, intuitive concept of an effective procedure. If the Turing machines are made to model the computation of the values of a function whose domain of definition and whose range are sets of natural numbers, then one arrives at the concept of a computable function (on a Turing machine). See also Turing machine.
Partial recursive functions.
All known examples of algorithms may be reduced to the problem of computing the values of a suitable function. Taking this feature as the fundamental property, Church, Gödel and Kleene defined a wide class of functions, which they named partial recursive. Let $F$ be the class of partial functions, with domains of definition and ranges of values in the set of natural numbers. The following operations are defined on the set $F$:
a) superposition (composition) of functions: If $f,\alpha_1,\ldots,a_m \in F$, then one says that the function $$ \phi(x_1,\ldots,x_n) = f(\alpha_1(x_1,\ldots,x_n),\ldots,\alpha_m(x_1,\ldots,x_n)) $$ is obtained from $f,\alpha_1,\ldots,a_m$ by composition;
b) the $\mu$ or least-number operator: Let $f_1,f_2 \in F$; one says that a function $\psi$ is obtained from $f_1$ and $f_2$ with the aid of the $\mu$-operator, written as $$ \psi(x_1,\ldots,x_n) = \mu y [f_1,f_2,(x_1,\ldots,x_n),y] $$ if $f_1(x_1,\ldots,x_n,z)$ and $f_2(x_1,\ldots,x_n,z)$ are defined and are unequal for $z<y$ and if $$ f_1(x_1,\ldots,x_n,y) = f_2(x_1,\ldots,x_n,y) $$ and then $$ \psi(x_1,\ldots,x_n) = y \ . $$
Clearly, if these operations are applied to functions the values of which one can compute, then there exist algorithms for computing the values of the functions $\phi$ and $\psi$. The following functions are considered to be the simplest: ${+},{\times}$, $\mathrm{pr}_i : ( x_1,\ldots,x_n) \mapsto x_i$, and $$ k(x,y) = \begin{cases} 1 & \ \text{if}\ x < y \\ 0 & \ \text{otherwise} \end{cases} \ . $$
There exist easy algorithms which serve to compute the values of the simplest functions.
A function $f$ is called partial recursive if it can be obtained by a finite number of steps from the simplest functions using the composition and the $\mu$-operator. A partial recursive function which is everywhere defined is called general recursive. The value of any partial recursive function may be effectively computed in the intuitive sense. The converse of this statement is known as Church's thesis: Any function the value of which can be effectively computed is partial recursive. Thus, according to Church's thesis, computable functions are partial recursive.
The normal algorithms of Markov.
Any given algorithm involves a certain alphabet, and the solution of a given problem is reduced to the processing of the words over this alphabet according to certain rules specified in advance. This approach to the theory of algorithms was developed by Markov, who presented the concept of a normal algorithm as the mathematical model of the concept of a computational procedure.
A normal algorithm  consists of a certain alphabet
consists of a certain alphabet 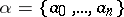 and a finite ordered list of rules of the form
and a finite ordered list of rules of the form 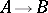 , where
, where 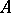 and
and 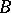 are certain words over the alphabet
are certain words over the alphabet 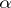 . Some of the rules are distinguished as final. A rule
. Some of the rules are distinguished as final. A rule  is applied to a word
is applied to a word 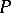 as follows: The word
as follows: The word 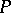 is represented in the form
is represented in the form 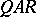 , where
, where 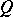 and
and  are words over the alphabet
are words over the alphabet  which may also be empty; out of all such representations the one in which the word
which may also be empty; out of all such representations the one in which the word 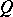 is shortest is selected, and the result of the application of this rule to the word
is shortest is selected, and the result of the application of this rule to the word 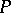 is said to be the word
is said to be the word  . A normal algorithm
. A normal algorithm 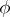 is applied to the word
is applied to the word 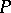 as follows: The first rule which is applicable to the word
as follows: The first rule which is applicable to the word 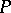 is applied, so a word
is applied, so a word 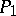 is obtained; the first rule which is applicable to the word
is obtained; the first rule which is applicable to the word 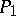 is applied, so a word
is applied, so a word 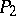 is obtained, etc. The result is a sequence of words which terminates after some final rule has been applied.
is obtained, etc. The result is a sequence of words which terminates after some final rule has been applied.
If the information is suitably coded, normal algorithms may be applied to the solution of various algorithmic problems. Any computational procedure modelled on a normal algorithm is effective in the intuitive sense. The converse of this statement is known as Markov's thesis: Any effective computational procedure can be modelled by a suitable normal algorithm. If the computation of the values of functions in the class 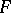 is modelled by normal algorithms, another concept of a computable function is obtained. Other more precise definitions of the concept of algorithms have been proposed (cf. Algorithm; Normal algorithm).
is modelled by normal algorithms, another concept of a computable function is obtained. Other more precise definitions of the concept of algorithms have been proposed (cf. Algorithm; Normal algorithm).
The following result on the equivalence of the various conceptions of the notion of algorithm has been demonstrated: The classes of functions computable on Turing machines and the partial recursive functions which are computable by Markov's normal algorithms (or similar classes of functions for other conceptions of the notion of algorithm) are identical. In the view of most mathematicians of our time, this class of functions may serve as the class of intuitively computable functions and is identified with it. Such an identification makes it possible to treat algorithmic problems as mathematical problems.
References
| [1] | A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [2] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
| [3] | A.M. Turing, "On computable numbers, with an application to the Entscheidungsproblem" Proc. London Math. Soc. (2) , 42 (1937) pp. 230–265 |
| [4] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [5] | A.A. Markov, "Theory of algorithms" , Israel Program Sci. Transl. (1961) (Translated from Russian) (Also: Trudy Mat. Inst. Steklov. 42 (1954)) |
Comments
The "symbols of motion" 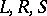 stand for "left" , "right" and "no move" ( "stand" ), respectively.
stand for "left" , "right" and "no move" ( "stand" ), respectively.
More information can be found in the article Mathematical theory of computation.
Computable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Computable_function&oldid=41830