Difference between revisions of "Semi-continuous mapping"
(Importing text file) |
m (link) |
||
| Line 9: | Line 9: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840205.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840205.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840206.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840207.png" />) denotes the limes superior (inferior). | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840206.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084020/s0840207.png" />) denotes the [[limes superior]] (inferior). |
Revision as of 13:13, 8 May 2017
upper (lower)
A mapping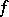 
from a topological space 
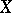into a partially ordered set 
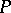such that
 |
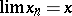implies that
 |
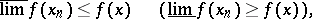where 
(
) denotes the limes superior (inferior).
Comments
On a partially ordered set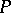 
the collection consisting of 
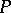and all sets 
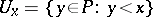is a base for a topology on 
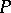, denoted by 
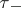, and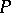 
and all sets 
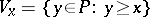define a topology 
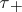. The mapping 
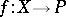is upper semi-continuous, (u.s.c.) (respectively, lower semi-continuous (l.s.c.)) if and only if 
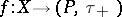(respectively, 
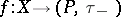) is continuous.
In fact, upper and lower semi-continuity are usually defined only for mappings to the real line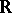 
. In terms of open sets, one sees that 
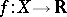is upper (lower) semi-continuous if and only if 
(
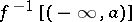) is open for every 
.
Semi-continuity is also defined for set-valued mappings. A mapping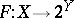 
is upper (lower) semi-continuous if for every open subset 
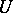of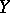 
the set 
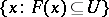(the set 
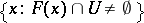) is open.
Note that if a mapping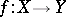 
is regarded as a set-valued mapping 
, 
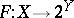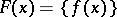, then 
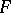is lower semi-continuous if and only if 
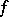is lower semi-continuous; and 
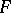is upper semi-continuous if and only if 
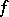is upper semi-continuous.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Semi-continuous mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-continuous_mapping&oldid=41325