Difference between revisions of "Cokernel"
(Importing text file) |
m (link) |
||
| Line 9: | Line 9: | ||
Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319017.png" /> is an isomorphism, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319018.png" /> is a cokernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319019.png" />. Thus, all cokernels of a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319020.png" /> form a quotient object of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319021.png" />, which is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319022.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319023.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319024.png" /> is a normal epimorphism. The converse need not be true. The cokernel of the zero morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319025.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319026.png" />. The cokernel of the unit morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319027.png" /> exists if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319028.png" /> contains a zero object. | Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319017.png" /> is an isomorphism, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319018.png" /> is a cokernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319019.png" />. Thus, all cokernels of a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319020.png" /> form a quotient object of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319021.png" />, which is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319022.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319023.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319024.png" /> is a normal epimorphism. The converse need not be true. The cokernel of the zero morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319025.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319026.png" />. The cokernel of the unit morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319027.png" /> exists if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319028.png" /> contains a zero object. | ||
| − | In a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319029.png" /> with a zero object, a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319030.png" /> has a cokernel if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319031.png" /> contains a co-Cartesian square with respect to the morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319033.png" />. This condition is satisfied, in particular, for any morphism of a right locally small category with a zero object and products. | + | In a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319029.png" /> with a zero object, a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319030.png" /> has a cokernel if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319031.png" /> contains a co-Cartesian square with respect to the morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023190/c02319033.png" />. This condition is satisfied, in particular, for any morphism of a right [[locally small category]] with a zero object and products. |
Revision as of 16:12, 29 October 2016
of a morphism in a category
The concept dual to the concept of the kernel of a morphism in a category. In categories of vector spaces, groups, rings, etc. it describes a largest quotient object of an object 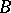 that annihilates the image of a homomorphism
that annihilates the image of a homomorphism  .
.
Let 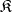 be a category with null morphisms. A morphism
be a category with null morphisms. A morphism 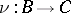 is called a cokernel of a morphism
is called a cokernel of a morphism 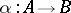 if
if 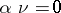 and if any morphism
and if any morphism 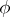 such that
such that 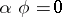 can be expressed in unique way as
can be expressed in unique way as  . A cokernel of a morphism
. A cokernel of a morphism 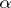 is denoted by
is denoted by 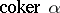 .
.
If  and
and 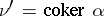 then
then 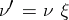 for a unique isomorphism
for a unique isomorphism 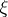 .
.
Conversely, if 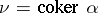 and
and 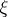 is an isomorphism, then
is an isomorphism, then 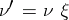 is a cokernel of
is a cokernel of 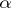 . Thus, all cokernels of a morphism
. Thus, all cokernels of a morphism 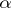 form a quotient object of
form a quotient object of 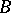 , which is denoted by
, which is denoted by 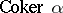 . If
. If  , then
, then  is a normal epimorphism. The converse need not be true. The cokernel of the zero morphism
is a normal epimorphism. The converse need not be true. The cokernel of the zero morphism  is
is 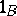 . The cokernel of the unit morphism
. The cokernel of the unit morphism  exists if and only if
exists if and only if 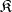 contains a zero object.
contains a zero object.
In a category 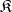 with a zero object, a morphism
with a zero object, a morphism 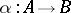 has a cokernel if and only if
has a cokernel if and only if 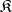 contains a co-Cartesian square with respect to the morphisms
contains a co-Cartesian square with respect to the morphisms 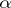 and
and 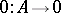 . This condition is satisfied, in particular, for any morphism of a right locally small category with a zero object and products.
. This condition is satisfied, in particular, for any morphism of a right locally small category with a zero object and products.
Comments
The co-Cartesian square, or fibred sum or pushout, of two morphisms  ,
,  is (if it exists) a commutative diagram
is (if it exists) a commutative diagram
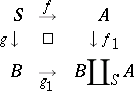 |
such that for any two morphisms  ,
, 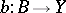 such that
such that 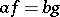 there exists a unique morphism
there exists a unique morphism 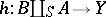 for which
for which 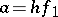 ,
, 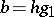 .
.
Cokernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cokernel&oldid=39517