Difference between revisions of "Base"
(Importing text file) |
(Tex partly done) |
||
| Line 1: | Line 1: | ||
| − | ''of a topological space | + | ''of a topological space $X$, base of a topology, basis of a topology, open base'' |
| − | A family | + | A family $\mathfrak{B}$ of open subsets of $X$ such that each open subset $G \subseteq X$ is a union of subcollections $U \subseteq \mathfrak{B}$. The concept of a base is a fundamental concept in topology: in many problems concerned with open sets of some space it is sufficient to restrict the considerations to its base. A space can have many bases, the largest one of which is the family of all open sets. The minimum of the cardinalities of all bases is called the ''[[Weight of a topological space|weight]]'' of the topological space $X$. In a space of weight $\tau$ there exists an everywhere-dense set of cardinality $\le \tau$. Spaces with a countable base are also referred to as spaces satisfying the [[second axiom of countability]]. The dual concept of a closed base, formed by the complements of the elements of a base, is used in [[compactification]] theory. |
| − | A local base of a space | + | A local base of a space $X$ at a point $x \in X$ (a base of the point $x$) is a family $\mathfrak{B}(x)$ of open sets of $X$ with the following property: For any neighbourhood $O_x$ of $x$ it is possible to find an element $V \in \mathfrak{B}(x)$ such that $x \in V \subseteq O_x$. Spaces with a countable local base at every point are also referred to as spaces satisfying the [[first axiom of countability]]. A family $\mathfrak{B}$ of open sets in $X$ is a base if and only if it is a local base of each one of its points $x \in X$. |
| − | Let | + | Let $\mathfrak{m}, \mathfrak{n}$ be cardinal numbers. A base $\mathfrak{B}$ of the space $X$ is called an $\mathfrak{m}$-point base if each point $x \in X$ belongs to at most $\mathfrak{m}$ elements of the family $\mathfrak{B}$; in particular, if $\mathfrak{m} = 1$, the base is called ''disjoint''; if $\mathfrak{m}$ is finite, it is called ''bounded point finite''; and if $\mathfrak{m} = \aleph_0$, it is called ''point countable''. |
A base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530032.png" /> of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530033.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530035.png" />-local if each point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530036.png" /> has a neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530037.png" /> intersecting with at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530038.png" /> elements of the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530039.png" />; in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530040.png" />, the base is referred to as discrete; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530041.png" /> is finite, it is called bounded locally finite; and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530042.png" />, it is called locally countable. A base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530043.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530045.png" />-point base (or an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530047.png" />-local base) if it is a union of a set of cardinality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530048.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530049.png" />-point (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530050.png" />-local) bases; examples are, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530051.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530053.png" />-disjoint, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530055.png" />-point finite, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530057.png" />-discrete and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530059.png" />-locally finite bases. | A base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530032.png" /> of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530033.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530035.png" />-local if each point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530036.png" /> has a neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530037.png" /> intersecting with at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530038.png" /> elements of the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530039.png" />; in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530040.png" />, the base is referred to as discrete; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530041.png" /> is finite, it is called bounded locally finite; and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530042.png" />, it is called locally countable. A base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530043.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530045.png" />-point base (or an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530047.png" />-local base) if it is a union of a set of cardinality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530048.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530049.png" />-point (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530050.png" />-local) bases; examples are, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530051.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530053.png" />-disjoint, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530055.png" />-point finite, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530057.png" />-discrete and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530059.png" />-locally finite bases. | ||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.S. [P.S. Uryson] Urysohn, , ''Works on topology and other fields of mathematics'' , '''1–2''' , Leningrad (1951) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.S. Aleksandrov, B.A. Pasynkov, "An introduction to the theory of topological spaces and general dimension theory" , Moscow (1973) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> P.S. [P.S. Uryson] Urysohn, , ''Works on topology and other fields of mathematics'' , '''1–2''' , Leningrad (1951) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> P.S. Aleksandrov, B.A. Pasynkov, "An introduction to the theory of topological spaces and general dimension theory" , Moscow (1973) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)</TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | + | Besides the notions of a bounded point-finite base and a bounded local-finite base one also uses that of a point-finite base and a local-finite base. A base (or any family of subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530097.png" />) is called point finite if every point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530098.png" /> belongs to finitely many members of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b01530099.png" />, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b015300100.png" /> is finite for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b015300101.png" />. Note that the families <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b015300102.png" /> can have arbitrary large finite cardinalities, in contrast to the definition of bounded point finiteness, when the cardinalities of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b015300103.png" /> are bounded by a fixed finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015300/b015300104.png" />. Similar remarks apply to local finiteness. | |
| − | + | {{TEX|part}} | |
Revision as of 19:19, 19 October 2016
of a topological space $X$, base of a topology, basis of a topology, open base
A family $\mathfrak{B}$ of open subsets of $X$ such that each open subset $G \subseteq X$ is a union of subcollections $U \subseteq \mathfrak{B}$. The concept of a base is a fundamental concept in topology: in many problems concerned with open sets of some space it is sufficient to restrict the considerations to its base. A space can have many bases, the largest one of which is the family of all open sets. The minimum of the cardinalities of all bases is called the weight of the topological space $X$. In a space of weight $\tau$ there exists an everywhere-dense set of cardinality $\le \tau$. Spaces with a countable base are also referred to as spaces satisfying the second axiom of countability. The dual concept of a closed base, formed by the complements of the elements of a base, is used in compactification theory.
A local base of a space $X$ at a point $x \in X$ (a base of the point $x$) is a family $\mathfrak{B}(x)$ of open sets of $X$ with the following property: For any neighbourhood $O_x$ of $x$ it is possible to find an element $V \in \mathfrak{B}(x)$ such that $x \in V \subseteq O_x$. Spaces with a countable local base at every point are also referred to as spaces satisfying the first axiom of countability. A family $\mathfrak{B}$ of open sets in $X$ is a base if and only if it is a local base of each one of its points $x \in X$.
Let $\mathfrak{m}, \mathfrak{n}$ be cardinal numbers. A base $\mathfrak{B}$ of the space $X$ is called an $\mathfrak{m}$-point base if each point $x \in X$ belongs to at most $\mathfrak{m}$ elements of the family $\mathfrak{B}$; in particular, if $\mathfrak{m} = 1$, the base is called disjoint; if $\mathfrak{m}$ is finite, it is called bounded point finite; and if $\mathfrak{m} = \aleph_0$, it is called point countable.
A base 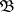 of the space
of the space 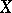 is called
is called 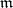 -local if each point
-local if each point 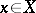 has a neighbourhood
has a neighbourhood 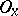 intersecting with at most
intersecting with at most 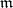 elements of the family
elements of the family 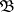 ; in particular, if
; in particular, if 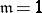 , the base is referred to as discrete; if
, the base is referred to as discrete; if 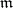 is finite, it is called bounded locally finite; and if
is finite, it is called bounded locally finite; and if 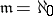 , it is called locally countable. A base
, it is called locally countable. A base 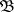 is called an
is called an 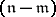 -point base (or an
-point base (or an 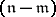 -local base) if it is a union of a set of cardinality
-local base) if it is a union of a set of cardinality  of
of 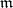 -point (
-point (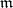 -local) bases; examples are, for
-local) bases; examples are, for 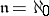 ,
, 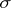 -disjoint,
-disjoint, 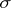 -point finite,
-point finite, 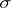 -discrete and
-discrete and 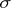 -locally finite bases.
-locally finite bases.
These concepts are used mainly in the criteria of metrizable spaces. Thus, a regular space with a countable base, or satisfying the first axiom of countability and with a point countable base, is metrizable; a regular space with a 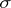 -discrete or
-discrete or 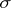 -locally finite base is metrizable (the converse proposition is true in the former case only).
-locally finite base is metrizable (the converse proposition is true in the former case only).
A base 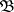 of the space
of the space 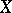 is called uniform (
is called uniform (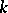 -uniform) if for each point
-uniform) if for each point 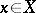 (each compact subset
(each compact subset 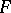 ) and for each one of the neighbourhoods
) and for each one of the neighbourhoods 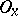 (
(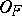 ) only a finite number of elements of the base contain
) only a finite number of elements of the base contain  (intersect with
(intersect with 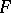 ) and at the same time intersect with the complement
) and at the same time intersect with the complement 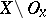 (
(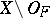 ). A space
). A space 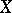 is metrizable if and only if it is paracompact with a uniform base (a Kolmogorov or
is metrizable if and only if it is paracompact with a uniform base (a Kolmogorov or 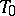 -space with a
-space with a 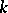 -uniform base).
-uniform base).
A base 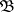 of the space
of the space 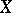 is called regular if for each point
is called regular if for each point 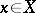 and an arbitrary neighbourhood
and an arbitrary neighbourhood 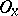 of it there exists a neighbourhood
of it there exists a neighbourhood 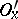 such that the set of all the elements of the base which intersect both with
such that the set of all the elements of the base which intersect both with 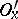 and
and 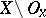 is finite. An accessible or
is finite. An accessible or 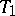 -space is metrizable if and only if it has a regular base.
-space is metrizable if and only if it has a regular base.
A generalization of the concept of a base is the so-called 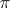 -base (lattice base), which is a family
-base (lattice base), which is a family 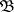 of open sets in the space
of open sets in the space 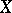 such that each non-empty open set in
such that each non-empty open set in 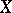 contains a non-empty set from
contains a non-empty set from  , i.e.
, i.e. 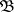 is dense in
is dense in 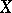 according to Hausdorff. All bases are
according to Hausdorff. All bases are 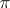 -bases, but the converse is not true; thus, the set
-bases, but the converse is not true; thus, the set 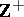 in the Stone–Čech compactification of the set of natural numbers in
in the Stone–Čech compactification of the set of natural numbers in 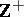 forms only a
forms only a 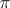 -base.
-base.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | P.S. [P.S. Uryson] Urysohn, , Works on topology and other fields of mathematics , 1–2 , Leningrad (1951) (In Russian) |
| [3] | P.S. Aleksandrov, B.A. Pasynkov, "An introduction to the theory of topological spaces and general dimension theory" , Moscow (1973) (In Russian) |
| [4] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [5] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
Comments
Besides the notions of a bounded point-finite base and a bounded local-finite base one also uses that of a point-finite base and a local-finite base. A base (or any family of subsets 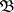 ) is called point finite if every point
) is called point finite if every point  belongs to finitely many members of
belongs to finitely many members of 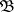 , i.e. if
, i.e. if 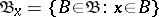 is finite for every
is finite for every  . Note that the families
. Note that the families 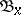 can have arbitrary large finite cardinalities, in contrast to the definition of bounded point finiteness, when the cardinalities of
can have arbitrary large finite cardinalities, in contrast to the definition of bounded point finiteness, when the cardinalities of 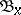 are bounded by a fixed finite
are bounded by a fixed finite 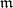 . Similar remarks apply to local finiteness.
. Similar remarks apply to local finiteness.
Base. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Base&oldid=39439