Difference between revisions of "*-regular ring"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A [[Regular ring (in the sense of von Neumann)|regular ring (in the sense of von Neumann)]] admitting an involutory anti-automorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770002.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770003.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770004.png" />. An idempotent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770005.png" /> of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770006.png" />-regular ring is called a projector if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770007.png" />. Every left (right) ideal of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770008.png" />-regular ring is generated by a unique projector. One can thus speak of the lattice of projectors of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770009.png" />-regular ring. If this lattice is complete, then it is a continuous geometry. A complemented [[Modular lattice|modular lattice]] (cf. also [[Lattice with complements|Lattice with complements]]) having a homogeneous basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700010.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700011.png" />, is an ortho-complemented lattice if and only if it is isomorphic to the lattice of projectors of some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700012.png" />-regular ring. | + | A [[Regular ring (in the sense of von Neumann)|regular ring (in the sense of von Neumann)]] admitting an involutory [[anti-automorphism]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770002.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770003.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770004.png" />. An idempotent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770005.png" /> of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770006.png" />-regular ring is called a projector if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770007.png" />. Every left (right) ideal of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770008.png" />-regular ring is generated by a unique projector. One can thus speak of the lattice of projectors of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r0770009.png" />-regular ring. If this lattice is complete, then it is a continuous geometry. A complemented [[Modular lattice|modular lattice]] (cf. also [[Lattice with complements|Lattice with complements]]) having a homogeneous basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700010.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700011.png" />, is an ortho-complemented lattice if and only if it is isomorphic to the lattice of projectors of some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700012.png" />-regular ring. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.K. Berberian, "Baer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700013.png" />-rings" , Springer (1972)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I. Kaplansky, "Rings of operators" , Benjamin (1968)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.K. Berberian, "Baer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077000/r07700013.png" />-rings" , Springer (1972)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I. Kaplansky, "Rings of operators" , Benjamin (1968)</TD></TR></table> | ||
Revision as of 17:12, 9 October 2016
A regular ring (in the sense of von Neumann) admitting an involutory anti-automorphism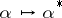 
such that 
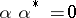implies 
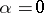. An idempotent 
of a 
-regular ring is called a projector if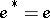 
. Every left (right) ideal of a 
-regular ring is generated by a unique projector. One can thus speak of the lattice of projectors of a 
-regular ring. If this lattice is complete, then it is a continuous geometry. A complemented modular lattice (cf. also Lattice with complements) having a homogeneous basis 
, where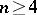 
, is an ortho-complemented lattice if and only if it is isomorphic to the lattice of projectors of some 
-regular ring.
References
| [1] | L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian) |
| [2] | S.K. Berberian, "Baer  -rings" , Springer (1972) |
| [3] | I. Kaplansky, "Rings of operators" , Benjamin (1968) |
How to Cite This Entry:
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=39393
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=39393
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article