Difference between revisions of "Acnode"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
An older term, hardly used nowadays (2000), for an isolated point, or hermit point, of a plane algebraic curve (cf. also [[Algebraic curve|Algebraic curve]]). | An older term, hardly used nowadays (2000), for an isolated point, or hermit point, of a plane algebraic curve (cf. also [[Algebraic curve|Algebraic curve]]). | ||
| Line 5: | Line 6: | ||
Figure: a130100a | Figure: a130100a | ||
| − | For instance, the point | + | For instance, the point $(0,0)$ is an acnode of the curve $X^3+X^2+Y^2=0$ in $\mathbf R^2$. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Walker, "Algebraic curves" , Princeton Univ. Press (1950) (Reprint: Dover 1962)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Walker, "Algebraic curves" , Princeton Univ. Press (1950) (Reprint: Dover 1962)</TD></TR></table> | ||
Revision as of 19:24, 20 July 2016
An older term, hardly used nowadays (2000), for an isolated point, or hermit point, of a plane algebraic curve (cf. also Algebraic curve).
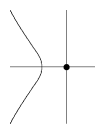
Figure: a130100a
For instance, the point $(0,0)$ is an acnode of the curve $X^3+X^2+Y^2=0$ in $\mathbf R^2$.
References
| [a1] | R.J. Walker, "Algebraic curves" , Princeton Univ. Press (1950) (Reprint: Dover 1962) |
How to Cite This Entry:
Acnode. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acnode&oldid=39018
Acnode. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acnode&oldid=39018
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article