Difference between revisions of "Cauchy filter"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A filter | + | A [[filter]] $\mathfrak{F}$ on a [[uniform space]] $X$ such that for any entourage $V$ of the uniform structure of $X$ there exists a set which is $V$-small and belongs to $\mathfrak{F}$. In other words, a Cauchy filter is a filter which contains arbitrarily small sets in a uniform space $X$. The concept is a generalization of the concept of a Cauchy sequence in metric spaces. |
| − | Every convergent filter is a Cauchy filter. Every filter which is finer than a Cauchy filter is also a Cauchy filter. The image of a Cauchy filterbase under a uniformly-continuous mapping is again a Cauchy filterbase. A uniform space in which every Cauchy filter is convergent is a complete space. | + | Every convergent filter (cf. [[Limit]]) is a Cauchy filter. Every filter which is finer than a Cauchy filter is also a Cauchy filter. The image of a Cauchy filterbase under a uniformly-continuous mapping is again a Cauchy filterbase. A uniform space in which every Cauchy filter is convergent is a [[complete space]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. II: Uniform structures (Translated from French)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. II: Uniform structures (Translated from French)</TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | A Cauchy filterbase (or Cauchy | + | A Cauchy filterbase (or Cauchy $d$-filterbase) is a filterbase <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086010.png" /> in a [[Metric space|metric space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086011.png" /> such that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086012.png" /> there is some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086013.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086014.png" /> (cf. [[#References|[a1]]]). |
A filterbase in a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086015.png" /> is a family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086016.png" /> of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086017.png" /> with the properties: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086018.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086019.png" />; and 2) for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086020.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086021.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086022.png" /> (see also [[Filter|Filter]]). | A filterbase in a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086015.png" /> is a family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086016.png" /> of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086017.png" /> with the properties: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086018.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086019.png" />; and 2) for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086020.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086021.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020860/c02086022.png" /> (see also [[Filter|Filter]]). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, "Topology" , Allyn & Bacon (1978)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, "Topology" , Allyn & Bacon (1978)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 16:43, 2 May 2016
A filter $\mathfrak{F}$ on a uniform space $X$ such that for any entourage $V$ of the uniform structure of $X$ there exists a set which is $V$-small and belongs to $\mathfrak{F}$. In other words, a Cauchy filter is a filter which contains arbitrarily small sets in a uniform space $X$. The concept is a generalization of the concept of a Cauchy sequence in metric spaces.
Every convergent filter (cf. Limit) is a Cauchy filter. Every filter which is finer than a Cauchy filter is also a Cauchy filter. The image of a Cauchy filterbase under a uniformly-continuous mapping is again a Cauchy filterbase. A uniform space in which every Cauchy filter is convergent is a complete space.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. II: Uniform structures (Translated from French) |
Comments
A Cauchy filterbase (or Cauchy $d$-filterbase) is a filterbase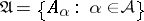 
in a metric space 
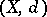such that for every 
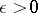there is some 
for which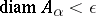 
(cf. [a1]).
A filterbase in a space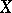 
is a family 
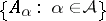of subsets of 
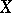with the properties: 1) 
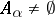for all 
; and 2) for all 
there is a 
such that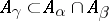 
(see also Filter).
References
| [a1] | J. Dugundji, "Topology" , Allyn & Bacon (1978) |
How to Cite This Entry:
Cauchy filter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_filter&oldid=38766
Cauchy filter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_filter&oldid=38766
This article was adapted from an original article by B.A. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article