Difference between revisions of "Kronecker symbol"
(Comment: also Legendre–Jacobi–Kronecker symbol) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
| − | + | ''Kronecker delta'' | |
| − | + | The number $\delta^i_j$ defined by | |
| + | $$ | ||
| + | \delta^i_j = \begin{cases} 1 & \text{if}\, i = j \\ 0 & \text{if}\, i \ne j \end{cases}\ \ , | ||
| + | $$ | ||
| + | $i,j = 1,2,\ldots$. When $1 \le i,j \le n$, the Kronecker symbol $\delta^i_j$ has $n^2$ components, and the matrix $(\delta^i_j)$ is the [[unit matrix]]. The Kronecker symbol was first used by L. Kronecker (1866). | ||
| − | + | The Kronecker symbol may be generalized, considering instead a set of quantities $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ with $2p$ integer (upper and lower) indices, $i_\alpha\,,j_\beta = 1,\ldots,n$, equal to $+1$ (or $-1$) if the sequence $(i_1\ldots i_p)$ is an even (odd) permutation of the distinct indices $(j_1\ldots j_p)$ and zero otherwise. The numbers $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ (when $p \ge 2$ often denoted by $\epsilon^{i_1\ldots i_p}_{j_1\ldots j_p}$) are called the ''components'' of the Kronecker symbol. An [[affine tensor]] of type $(p,p)$ whose components relative to some basis are equal to the components of the Kronecker symbol has the same components relative to any other basis. | |
| − | |||
| − | The Kronecker symbol may be generalized, considering instead a set of quantities | ||
The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant | The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant | ||
| Line 24: | Line 26: | ||
====Comment==== | ====Comment==== | ||
For the Kronecker symbol in number theory, see [[Legendre–Jacobi–Kronecker symbol]] | For the Kronecker symbol in number theory, see [[Legendre–Jacobi–Kronecker symbol]] | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 18:19, 13 January 2016
Kronecker delta
The number $\delta^i_j$ defined by $$ \delta^i_j = \begin{cases} 1 & \text{if}\, i = j \\ 0 & \text{if}\, i \ne j \end{cases}\ \ , $$ $i,j = 1,2,\ldots$. When $1 \le i,j \le n$, the Kronecker symbol $\delta^i_j$ has $n^2$ components, and the matrix $(\delta^i_j)$ is the unit matrix. The Kronecker symbol was first used by L. Kronecker (1866).
The Kronecker symbol may be generalized, considering instead a set of quantities $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ with $2p$ integer (upper and lower) indices, $i_\alpha\,,j_\beta = 1,\ldots,n$, equal to $+1$ (or $-1$) if the sequence $(i_1\ldots i_p)$ is an even (odd) permutation of the distinct indices $(j_1\ldots j_p)$ and zero otherwise. The numbers $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ (when $p \ge 2$ often denoted by $\epsilon^{i_1\ldots i_p}_{j_1\ldots j_p}$) are called the components of the Kronecker symbol. An affine tensor of type $(p,p)$ whose components relative to some basis are equal to the components of the Kronecker symbol has the same components relative to any other basis.
The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant
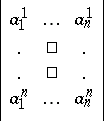 |
is equal to the sum
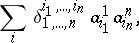 |
where the summation is performed over all  permutations of the numbers
permutations of the numbers 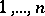 . The alternant of the tensor
. The alternant of the tensor  is given by
is given by
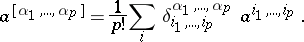 |
References
| [1] | L. Kronecker, "Vorlesungen über die Theorie der Determinanten" , Leipzig (1903) |
Comment
For the Kronecker symbol in number theory, see Legendre–Jacobi–Kronecker symbol
Kronecker symbol. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker_symbol&oldid=37518