Difference between revisions of "Formal power series"
(TeX partially done) |
(→Comments: TeX partially done) |
||
| Line 52: | Line 52: | ||
Power series in non-commuting variables are becoming rapidly more important and find applications in combinatorics (enumerative graph theory), computer science (automata) and system and control theory (representation of the input-output behaviour of non-linear systems, especially bilinear systems); cf. the collection [[#References|[a1]]] for a first idea. | Power series in non-commuting variables are becoming rapidly more important and find applications in combinatorics (enumerative graph theory), computer science (automata) and system and control theory (representation of the input-output behaviour of non-linear systems, especially bilinear systems); cf. the collection [[#References|[a1]]] for a first idea. | ||
| − | Let | + | Let $A'$ be a ring containing $A$ (or provided with a ring homomorphism $\phi : A \rightarrow A'$), let $\mathfrak{a}'$ be an ideal in $A'$ and suppose that $A'$ is complete in the $\mathfrak{a}'$-adic topology on $A'$. Let $x_1,\ldots,x_n$ be elements of $\mathfrak{a}'$. Then an expression |
| + | $$ | ||
| + | \sum_{ i_1,\ldots,i_n = 0 }^\infty c_{ i_1,\ldots,i_n } x_1^{i_1}\cdots x_n^{i_n} | ||
| + | $$ | ||
| − | + | where the $i_j$ range over $\mathbf{N} \cup \{0\} = \{0,1,2,\ldots \}$, $c_{ i_1,\ldots,i_n } \in A$, has a well-defined meaning in $A'$ (as the unique limit of the finite sums | |
| + | $$ | ||
| + | \sum_{ i_1,\ldots,i_n = 0 }^m c_{ i_1,\ldots,i_n } x_1^{i_1}\cdots x_n^{i_n} | ||
| + | $$ | ||
| − | |||
| − | + | as $m \rightarrow \infty$). Such an expression is also called a formal power series over $A$. Mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087086.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087087.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087088.png" />, defines a (continuous) homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087089.png" />. If this homomorphism is injective, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087090.png" /> are said to be analytically independent over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087091.png" />. | |
| − | |||
| − | as | ||
Let now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087092.png" /> be a field with a multiplicative norm on it (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087093.png" />), e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087094.png" /> with the usual norm or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087095.png" />, the rational field, with the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087096.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087097.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087098.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870101.png" />-adic valuation on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870102.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870103.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870104.png" /> is the exponent of the largest power of the prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870105.png" /> that divides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870106.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870107.png" />). Now consider all formal power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870108.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870109.png" /> such that there exists positive numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870110.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870111.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870112.png" />. These form a subring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870113.png" />, called the ring of convergent power series over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870114.png" /> and denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870115.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870116.png" />, but the latter notation also occurs for the ring of power series in non-commuting variables over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870117.png" />). The Weierstrass preparation theorem also holds in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870118.png" />. | Let now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087092.png" /> be a field with a multiplicative norm on it (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087093.png" />), e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087094.png" /> with the usual norm or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087095.png" />, the rational field, with the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087096.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087097.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f04087098.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870101.png" />-adic valuation on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870102.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870103.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870104.png" /> is the exponent of the largest power of the prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870105.png" /> that divides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870106.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870107.png" />). Now consider all formal power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870108.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870109.png" /> such that there exists positive numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870110.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870111.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870112.png" />. These form a subring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870113.png" />, called the ring of convergent power series over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870114.png" /> and denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870115.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870116.png" />, but the latter notation also occurs for the ring of power series in non-commuting variables over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870117.png" />). The Weierstrass preparation theorem also holds in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040870/f040870118.png" />. | ||
Revision as of 19:33, 7 December 2015
over a ring $A$ in commuting variables $T_1,\ldots,T_N$
An algebraic expression of the form $$ F = \sum_{k=0}^\infty F_k $$
where $F_k$ is a form of degree $k$ in $T_1,\ldots,T_N$ with coefficients in $A$. The minimal value of $k$ for which $F_k \ne 0$ is called the order of the series $F$, and the form $F_k$ is called the initial form of the series.
If $$ F = \sum_{k=0}^\infty F_k \ \ \text{and}\ \ G = \sum_{k=0}^\infty G_k $$ are two formal power series, then, by definition, $$ F + G = \sum_{k=0}^\infty F_k + G_k $$ and $$ F \cdot G = \sum_{k=0}^\infty H_k $$ where $$ H_k = \sum_{j=0}^k F_j G_{k-j} \ . $$
The set $A[[T_1,\ldots,T_N]]$ of all formal power series forms a ring under these operations.
A polynomial $F = \sum_{k=0}^n F_k$, where $F_k$ is a form of degree $k$, is identified with the formal power series $C = \sum_{k=0}^\infty C_k$ , where $C_k = F_k$ for $k \le n$ and $C_k = 0$ for $k > n$. This defines an imbedding $i$ of the polynomial ring $A[T_1,\ldots,T_N]$ into $A[[T_1,\ldots,T_N]]$. There is a topology defined on $A[[T_1,\ldots,T_N]]$ for which the ideals $$ I_n = \{ F = \sum_{k=0}^\infty F_k \ :\ F_k = 0 \ \text{for}\ k \le n \} $$ form a fundamental system of neighbourhoods of zero. This topology is separable, the ring $A[[T_1,\ldots,T_N]]$ is complete relative to it, and the image of $A[T_1,\ldots,T_N]$ under the imbedding $i$ is everywhere dense in $A[[T_1,\ldots,T_N]]$. Relative to this topology, a power series $F = \sum_{k=0}^\infty F_k$ is the limit of its partial sums $F = \sum_{k=0}^n F_k$.
Suppose that $A$ is a commutative ring with an identity. Then so is $A[[T_1,\ldots,T_N]]$. If $A$ is an integral domain, then so is $A[[T_1,\ldots,T_N]]$. A formal power series $F = \sum_{k=0}^\infty F_k$ is invertible in $A[[T_1,\ldots,T_N]]$ if and only if $F_0$ is invertible in $A$. If $A$ is Noetherian, then so is $A[[T_1,\ldots,T_N]]$. If $A$ is a local ring with maximal ideal $\mathfrak{m}$, then $A[[T_1,\ldots,T_N]]$ is a local ring with maximal ideal $\left\langle \mathfrak{m}, T_1,\ldots,T_N \right\rangle$ .
If a local ring $A$ is separable and complete in the $\mathfrak{m}$-adic topology, then the Weierstrass preparation theorem is true in $A[[T_1,\ldots,T_N]]$. Let $F$ be a formal power series such that for some $k$ the form $F_k$ contains a term $a T^k$, where $a \notin \mathfrak{m}$, and let $k$ be the minimal index with this property. Then $F = UP$, where $U$ is an invertible formal power series and $P$ is a polynomial of the form $T^k + a_{k-1}T^{k-1} + \cdots + a_0$, where the coefficients $a_i$ belong to the maximal ideal of $A[[T_1,\ldots,T_N]]$. The elements $U$ and $P$ are uniquely determined by $F$.
The ring of formal power series over a field or a discretely-normed ring is factorial.
Rings of formal power series in non-commuting variables have also been studied.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , v. Nostrand (1960) |
Comments
Power series in non-commuting variables are becoming rapidly more important and find applications in combinatorics (enumerative graph theory), computer science (automata) and system and control theory (representation of the input-output behaviour of non-linear systems, especially bilinear systems); cf. the collection [a1] for a first idea.
Let $A'$ be a ring containing $A$ (or provided with a ring homomorphism $\phi : A \rightarrow A'$), let $\mathfrak{a}'$ be an ideal in $A'$ and suppose that $A'$ is complete in the $\mathfrak{a}'$-adic topology on $A'$. Let $x_1,\ldots,x_n$ be elements of $\mathfrak{a}'$. Then an expression $$ \sum_{ i_1,\ldots,i_n = 0 }^\infty c_{ i_1,\ldots,i_n } x_1^{i_1}\cdots x_n^{i_n} $$
where the $i_j$ range over $\mathbf{N} \cup \{0\} = \{0,1,2,\ldots \}$, $c_{ i_1,\ldots,i_n } \in A$, has a well-defined meaning in $A'$ (as the unique limit of the finite sums $$ \sum_{ i_1,\ldots,i_n = 0 }^m c_{ i_1,\ldots,i_n } x_1^{i_1}\cdots x_n^{i_n} $$
as $m \rightarrow \infty$). Such an expression is also called a formal power series over $A$. Mapping 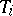 to
to 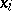 ,
, 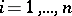 , defines a (continuous) homomorphism
, defines a (continuous) homomorphism 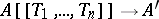 . If this homomorphism is injective, the
. If this homomorphism is injective, the  are said to be analytically independent over
are said to be analytically independent over 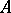 .
.
Let now 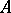 be a field with a multiplicative norm on it (i.e.
be a field with a multiplicative norm on it (i.e.  ), e.g.
), e.g. 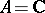 with the usual norm or
with the usual norm or 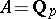 , the rational field, with the norm
, the rational field, with the norm 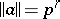 if
if 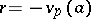 , where
, where 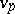 is the
is the 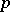 -adic valuation on
-adic valuation on 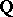 (
(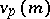 for
for 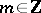 is the exponent of the largest power of the prime number
is the exponent of the largest power of the prime number 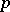 that divides
that divides 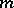 ;
; 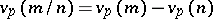 ). Now consider all formal power series
). Now consider all formal power series 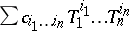 over
over 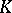 such that there exists positive numbers
such that there exists positive numbers  and
and  such that
such that 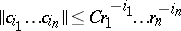 . These form a subring of
. These form a subring of 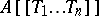 , called the ring of convergent power series over
, called the ring of convergent power series over 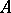 and denoted by
and denoted by 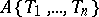 (or
(or 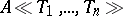 , but the latter notation also occurs for the ring of power series in non-commuting variables over
, but the latter notation also occurs for the ring of power series in non-commuting variables over  ). The Weierstrass preparation theorem also holds in
). The Weierstrass preparation theorem also holds in 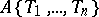 .
.
References
| [a1] | J. Berstel (ed.) , Series formelles en variables noncommutatives et aplications , Lab. Inform. Théor. Programmation (1978) |
| [a2] | M. Nagata, "Local rings" , Interscience (1960) |
Formal power series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_power_series&oldid=36862