Euler constant

The number $\gamma$ defined by

$$ \gamma=\lim_{n\to \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\ln n\right)\approx 0.57721566490\ldots,$$

considered by L. Euler (1740). Its existence follows from the fact that the sequence

$$ 1+\frac{1}{2}+\cdots+\frac{1}{n}-\ln(n+1)$$

is monotone increasing and bounded from above. The number-theoretic nature of the Euler constant has not been studied; it is not even known (2012) whether it is a rational number or not.

In fact, a relation

$$ \sum_{n\leq x}\,\frac{1}{n}-\ln x=\gamma+O\left(\frac{1}{x}\right)$$

holds, cf. [HaWr, Chapter 22.5].

References

[HaWr]

G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 MR0568909 Zbl 0423.10001

Comments

Also known as the Euler-Mascheroni constant, after L. Euler (1707–1783) and L. Mascheroni (1750–1800).

References

[Fi]	Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications 94, Cambridge University Press (2003) ISBN 0-521-81805-2 Zbl 1054.00001

Comments

Indeed, one also has

(a13)

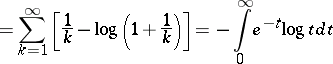and

(a14)

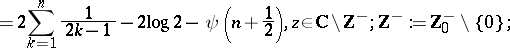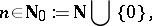where an empty sum is interpreted, as usual, to be zero. In terms of the Riemann zeta-function 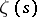, Euler's classical results state:

(a15)

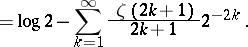References

[a1]	A. Erdélyi, W. Magnus, F. Oberhettinger, F.G. Tricomi, "Higher transcendental functions" , I , McGraw-Hill (1953)
[a2]	L. Lewin, "Polylogarithms and associated functions" , Elsevier (1981)
[a3]	H.M. Srivastava, J. Choi, "Series associated with the zeta and related functions" , Kluwer Acad. Publ. (2001)