Difference between revisions of "Euler constant"
(Also known as the ''Euler-Mascheroni'' constant, cite Finch (2003)) |
(moved text from Catalan constant) |
||
| Line 1: | Line 1: | ||
| − | {{TEX| | + | {{TEX|part}} |
The number $\gamma$ defined by | The number $\gamma$ defined by | ||
| Line 24: | Line 24: | ||
====Comments==== | ====Comments==== | ||
| − | Also known as the ''Euler-Mascheroni'' constant. | + | Also known as the ''Euler-Mascheroni'' constant, after L. Euler (1707–1783) and L. Mascheroni (1750–1800). |
====References==== | ====References==== | ||
{| | {| | ||
|- | |- | ||
| − | |valign="top"|{{Ref|Fi}}||valign="top"| Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications '''94''', Cambridge University Press (2003) ISBN 0-521-81805-2 | + | |valign="top"|{{Ref|Fi}}||valign="top"| Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications '''94''', Cambridge University Press (2003) ISBN 0-521-81805-2 {{ZBL|1054.00001}} |
|- | |- | ||
|} | |} | ||
| + | |||
| + | ====Comments==== | ||
| + | ==Euler–Mascheroni constant.== | ||
| + | Indeed, one also has | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004037.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a13)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004038.png" /></td> </tr></table> | ||
| + | |||
| + | and | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004039.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a14)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004040.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004041.png" /></td> </tr></table> | ||
| + | |||
| + | where an empty sum is interpreted, as usual, to be zero. In terms of the Riemann zeta-function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004042.png" />, Euler's classical results state: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004043.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a15)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004044.png" /></td> </tr></table> | ||
| + | |||
| + | ====References==== | ||
| + | <table> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Erdélyi, W. Magnus, F. Oberhettinger, F.G. Tricomi, "Higher transcendental functions" , '''I''' , McGraw-Hill (1953)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Lewin, "Polylogarithms and associated functions" , Elsevier (1981)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> H.M. Srivastava, J. Choi, "Series associated with the zeta and related functions" , Kluwer Acad. Publ. (2001)</TD></TR> | ||
| + | </table> | ||
Revision as of 19:09, 29 December 2014
The number $\gamma$ defined by
$$ \gamma=\lim_{n\to \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\ln n\right)\approx 0.57721566490\ldots,$$
considered by L. Euler (1740). Its existence follows from the fact that the sequence
$$ 1+\frac{1}{2}+\cdots+\frac{1}{n}-\ln(n+1)$$
is monotone increasing and bounded from above. The number-theoretic nature of the Euler constant has not been studied; it is not even known (2012) whether it is a rational number or not.
In fact, a relation
$$ \sum_{n\leq x}\,\frac{1}{n}-\ln x=\gamma+O\left(\frac{1}{x}\right)$$
holds, cf. [HaWr, Chapter 22.5].
References
| [HaWr] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 MR0568909 Zbl 0423.10001 |
Comments
Also known as the Euler-Mascheroni constant, after L. Euler (1707–1783) and L. Mascheroni (1750–1800).
References
| [Fi] | Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications 94, Cambridge University Press (2003) ISBN 0-521-81805-2 Zbl 1054.00001 |
Comments
Euler–Mascheroni constant.
Indeed, one also has
 | (a13) |
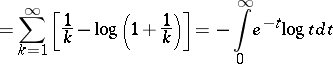 |
and
 | (a14) |
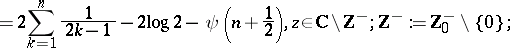 |
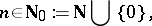 |
where an empty sum is interpreted, as usual, to be zero. In terms of the Riemann zeta-function 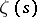 , Euler's classical results state:
, Euler's classical results state:
 | (a15) |
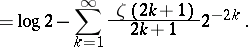 |
References
| [a1] | A. Erdélyi, W. Magnus, F. Oberhettinger, F.G. Tricomi, "Higher transcendental functions" , I , McGraw-Hill (1953) |
| [a2] | L. Lewin, "Polylogarithms and associated functions" , Elsevier (1981) |
| [a3] | H.M. Srivastava, J. Choi, "Series associated with the zeta and related functions" , Kluwer Acad. Publ. (2001) |
Euler constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_constant&oldid=35954