Difference between revisions of "Dirichlet convolution"
(Importing text file) |
(LaTeX) |
||
| Line 1: | Line 1: | ||
| − | The Dirichlet convolution of two | + | The Dirichlet convolution of two [[arithmetic function]]s $f(n)$ and $g(n)$ is defined as |
| + | $$ | ||
| + | (f*g)(n) = \sum_{d|n} f(d) g(n/d) \ , | ||
| + | $$ | ||
| + | where the sum is over the positive divisors $d$ of $n$. General background material on the Dirichlet convolution can be found in, e.g., [[#References|[a1]]], [[#References|[a6]]], [[#References|[a8]]]. | ||
| − | + | Sums of the form $\sum_{d|n} f(d) g(n/d)$ played an important role from the very beginning of the theory of arithmetical functions. Many results from early times involved these sums. For example, in 1857 J. Liouville published a long list of arithmetical identities of this type (see [[#References|[a5]]]). It is fruitful to treat the sums $\sum_{d|n} f(d) g(n/d)$ as giving a binary operation on the set of arithmetical functions (cf. also [[Binary relation]]). This aspect was introduced by E.T. Bell [[#References|[a2]]] and M. Cipolla [[#References|[a3]]] in 1915. | |
| − | + | The set of arithmetical functions forms a [[commutative ring]] with unity under the usual addition and the Dirichlet convolution. An arithmetical function $f$ possesses a Dirichlet inverse if and only if $f(1) /neq 0$. For example, the Dirichlet inverse of the constant function 1 is the [[Möbius function]] $\mu$. The [[Möbius inversion]] formula states that | |
| + | $$ | ||
| + | f(n) = \sum_{d|n} g(d) \Leftrightarrow g(n) = \sum_{d|n} \mu(d) f(n/d) \ . | ||
| + | $$ | ||
| − | + | The relation of the Dirichlet convolution with [[Dirichlet series]] is also important. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The relation of the Dirichlet convolution with [[ | ||
There are many analogues and generalizations of the Dirichlet convolution; for example, E. Cohen [[#References|[a4]]] defined the unitary convolution as | There are many analogues and generalizations of the Dirichlet convolution; for example, E. Cohen [[#References|[a4]]] defined the unitary convolution as | ||
| − | + | $$ | |
| − | + | (f \times g)(n) = \sum_{d \Vert n} f(d) g(n/d) \ , | |
| − | + | $$ | |
| − | where the sum is over the positive divisors | + | where the sum is over the [[unitary divisor]]s of $n$: the positive divisors $d$ of $n$ such that $\mathrm{hcf}(d,n/d) = 1$, see also [[#References|[a10]]]. W. Narkiewicz [[#References|[a7]]] developed a more general convolution: |
| − | + | $$ | |
| + | (f *_A g)(n) = \sum_{d \in A(n)} f(d) g(n/d) \ , | ||
| + | $$ | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130150/d13015016.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130150/d13015016.png" /></td> </tr></table> | ||
| − | where, for each | + | where, for each $n$, $A(n)$ is a subset of the set of the positive divisors of $n$. See [[#References|[a9]]] for a survey of various binary operations on the set of arithmetical functions. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Introduction to analytic number theory" , Springer (1976)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E.T. Bell, "An arithmetical theory of certain numerical functions" ''Univ. Wash. Publ. Math. Phys. Sci.'' , '''I''' : 1 (1915)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Cipolla, "Sui principi del calculo arithmetico integrale" ''Atti Accad. Gioenia Cantonia'' , '''5''' : 8 (1915)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Cohen, "Arithmetical functions associated with the unitary divisors of an integer" ''Math. Z.'' , '''74''' (1960) pp. 66–80</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L.E. Dickson, "History of the theory of numbers" , '''I''' , Chelsea, reprint (1952)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P.J. McCarthy, "Introduction to arithmetical functions" , Springer (1986)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Narkiewicz, "On a class of arithmetical convolutions" ''Colloq. Math.'' , '''10''' (1963) pp. 81–94</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Sivaramakrishnan, "Classical theory of arithmetic functions" , ''Monographs and Textbooks in Pure and Applied Math.'' , '''126''' , M. Dekker (1989)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M.V. Subbarao, "On some arithmetic convolutions" , ''The Theory of Arithmetic Functions'' , ''Lecture Notes in Mathematics'' , '''251''' , Springer (1972) pp. 247–271</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> R. Vaidyanathaswamy, "The theory of multiplicative arithmetic functions" ''Trans. Amer. Math. Soc.'' , '''33''' (1931) pp. 579–662</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Introduction to analytic number theory" , Springer (1976)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> E.T. Bell, "An arithmetical theory of certain numerical functions" ''Univ. Wash. Publ. Math. Phys. Sci.'' , '''I''' : 1 (1915)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Cipolla, "Sui principi del calculo arithmetico integrale" ''Atti Accad. Gioenia Cantonia'' , '''5''' : 8 (1915)</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Cohen, "Arithmetical functions associated with the unitary divisors of an integer" ''Math. Z.'' , '''74''' (1960) pp. 66–80</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> L.E. Dickson, "History of the theory of numbers" , '''I''' , Chelsea, reprint (1952)</TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> P.J. McCarthy, "Introduction to arithmetical functions" , Springer (1986)</TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Narkiewicz, "On a class of arithmetical convolutions" ''Colloq. Math.'' , '''10''' (1963) pp. 81–94</TD></TR> | ||
| + | <TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Sivaramakrishnan, "Classical theory of arithmetic functions" , ''Monographs and Textbooks in Pure and Applied Math.'' , '''126''' , M. Dekker (1989)</TD></TR> | ||
| + | <TR><TD valign="top">[a9]</TD> <TD valign="top"> M.V. Subbarao, "On some arithmetic convolutions" , ''The Theory of Arithmetic Functions'' , ''Lecture Notes in Mathematics'' , '''251''' , Springer (1972) pp. 247–271</TD></TR> | ||
| + | <TR><TD valign="top">[a10]</TD> <TD valign="top"> R. Vaidyanathaswamy, "The theory of multiplicative arithmetic functions" ''Trans. Amer. Math. Soc.'' , '''33''' (1931) pp. 579–662</TD></TR> | ||
| + | </table> | ||
Revision as of 22:26, 11 December 2014
The Dirichlet convolution of two arithmetic functions $f(n)$ and $g(n)$ is defined as $$ (f*g)(n) = \sum_{d|n} f(d) g(n/d) \ , $$ where the sum is over the positive divisors $d$ of $n$. General background material on the Dirichlet convolution can be found in, e.g., [a1], [a6], [a8].
Sums of the form $\sum_{d|n} f(d) g(n/d)$ played an important role from the very beginning of the theory of arithmetical functions. Many results from early times involved these sums. For example, in 1857 J. Liouville published a long list of arithmetical identities of this type (see [a5]). It is fruitful to treat the sums $\sum_{d|n} f(d) g(n/d)$ as giving a binary operation on the set of arithmetical functions (cf. also Binary relation). This aspect was introduced by E.T. Bell [a2] and M. Cipolla [a3] in 1915.
The set of arithmetical functions forms a commutative ring with unity under the usual addition and the Dirichlet convolution. An arithmetical function $f$ possesses a Dirichlet inverse if and only if $f(1) /neq 0$. For example, the Dirichlet inverse of the constant function 1 is the Möbius function $\mu$. The Möbius inversion formula states that $$ f(n) = \sum_{d|n} g(d) \Leftrightarrow g(n) = \sum_{d|n} \mu(d) f(n/d) \ . $$
The relation of the Dirichlet convolution with Dirichlet series is also important.
There are many analogues and generalizations of the Dirichlet convolution; for example, E. Cohen [a4] defined the unitary convolution as $$ (f \times g)(n) = \sum_{d \Vert n} f(d) g(n/d) \ , $$ where the sum is over the unitary divisors of $n$: the positive divisors $d$ of $n$ such that $\mathrm{hcf}(d,n/d) = 1$, see also [a10]. W. Narkiewicz [a7] developed a more general convolution: $$ (f *_A g)(n) = \sum_{d \in A(n)} f(d) g(n/d) \ , $$
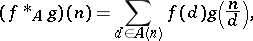 |
where, for each $n$, $A(n)$ is a subset of the set of the positive divisors of $n$. See [a9] for a survey of various binary operations on the set of arithmetical functions.
References
| [a1] | T.M. Apostol, "Introduction to analytic number theory" , Springer (1976) |
| [a2] | E.T. Bell, "An arithmetical theory of certain numerical functions" Univ. Wash. Publ. Math. Phys. Sci. , I : 1 (1915) |
| [a3] | M. Cipolla, "Sui principi del calculo arithmetico integrale" Atti Accad. Gioenia Cantonia , 5 : 8 (1915) |
| [a4] | E. Cohen, "Arithmetical functions associated with the unitary divisors of an integer" Math. Z. , 74 (1960) pp. 66–80 |
| [a5] | L.E. Dickson, "History of the theory of numbers" , I , Chelsea, reprint (1952) |
| [a6] | P.J. McCarthy, "Introduction to arithmetical functions" , Springer (1986) |
| [a7] | W. Narkiewicz, "On a class of arithmetical convolutions" Colloq. Math. , 10 (1963) pp. 81–94 |
| [a8] | R. Sivaramakrishnan, "Classical theory of arithmetic functions" , Monographs and Textbooks in Pure and Applied Math. , 126 , M. Dekker (1989) |
| [a9] | M.V. Subbarao, "On some arithmetic convolutions" , The Theory of Arithmetic Functions , Lecture Notes in Mathematics , 251 , Springer (1972) pp. 247–271 |
| [a10] | R. Vaidyanathaswamy, "The theory of multiplicative arithmetic functions" Trans. Amer. Math. Soc. , 33 (1931) pp. 579–662 |
Dirichlet convolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_convolution&oldid=35562