Difference between revisions of "Complementation"
(Importing text file) |
(LaTeX part) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|part}} | |
| − | + | An operation which brings a subset $M$ of a given set $X$ into correspondence with another subset $N$ so that if $M$ and $N$ are known, it is possible in some way to reproduce $X$. Depending on the structure with which $X$ is endowed, one distinguishes various definitions of complementation, as well as various methods of reconstituting $X$ from $M$ and $N$. | |
| − | + | ===Sets=== | |
| + | In the general theory of sets the complement of a subset $M$ (or complementary subset, relative complement) in a set $X$ is the subset $\complement_X M$ (or $\complement M$ if $X$ is assumed, or $X \setminus M$) consisting of all elements $x \in X$ not belonging to $M$; an important property is the [[duality principle]] (one of the [[De Morgan laws]]): | ||
| + | $$ | ||
| + | \complement \bigcup_{\xi} M_\xi = \bigcap_\xi \complement M_\xi | ||
| + | $$ | ||
| − | + | ===Linear spaces=== | |
| + | Let $X$ have a structure of a [[linear space]] and let $M$ be a subspace of $X$. A subspace $N \subset X$ is said to be a direct algebraic complement (or '''algebraic complement''', for short) of $M$ if any $x \in X$ can be uniquely represented as $x = y+z$, $y \in M$, $z \in N$. This is equivalent to the conditions $X = M + N$; $M \cap N = \{0\}$. Any subspace of $X$ has an algebraic complement, but this complement is not uniquely determined. | ||
| + | ===Linear topological spaces=== | ||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369031.png" /> be a linear topological space and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369032.png" /> be the direct algebraic sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369033.png" /> of its subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369035.png" />, regarded as linear topological spaces with the induced topology. The one-to-one mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369036.png" /> of the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369037.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369038.png" />, which is continuous by virtue of the linearity of the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369039.png" />, does not have, in general, a continuous inverse. If this mapping is a homeomorphism, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369040.png" /> is the direct topological sum of the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369042.png" />, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369043.png" /> is said to be the direct topological complement of the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369044.png" />, the latter being known as a complementable subspace. Not all subspaces in an arbitrary linear topological space, not even the finite-dimensional ones, are complementable. The following necessary and sufficient condition for complementability holds: The subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369045.png" /> is topologically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369046.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369047.png" /> is an algebraic complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369048.png" />. This criterion entails the following sufficient conditions for complementability: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369049.png" /> is closed and has finite codimension; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369050.png" /> is locally convex and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369051.png" /> is finite-dimensional; etc. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369031.png" /> be a linear topological space and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369032.png" /> be the direct algebraic sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369033.png" /> of its subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369035.png" />, regarded as linear topological spaces with the induced topology. The one-to-one mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369036.png" /> of the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369037.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369038.png" />, which is continuous by virtue of the linearity of the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369039.png" />, does not have, in general, a continuous inverse. If this mapping is a homeomorphism, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369040.png" /> is the direct topological sum of the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369042.png" />, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369043.png" /> is said to be the direct topological complement of the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369044.png" />, the latter being known as a complementable subspace. Not all subspaces in an arbitrary linear topological space, not even the finite-dimensional ones, are complementable. The following necessary and sufficient condition for complementability holds: The subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369045.png" /> is topologically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369046.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369047.png" /> is an algebraic complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369048.png" />. This criterion entails the following sufficient conditions for complementability: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369049.png" /> is closed and has finite codimension; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369050.png" /> is locally convex and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369051.png" /> is finite-dimensional; etc. | ||
| + | ===Hilbert spaces=== | ||
A special case of topological complementation is the orthogonal complement of a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369052.png" /> of a Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369053.png" />. This is the set | A special case of topological complementation is the orthogonal complement of a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369052.png" /> of a Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369053.png" />. This is the set | ||
| Line 15: | Line 22: | ||
which is a closed subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369055.png" />. An important fact in the theory of Hilbert spaces is that any closed subspace of a Hilbert space has an orthogonal complement, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369056.png" />. | which is a closed subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369055.png" />. An important fact in the theory of Hilbert spaces is that any closed subspace of a Hilbert space has an orthogonal complement, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369056.png" />. | ||
| + | ===Vector lattices=== | ||
Finally, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369057.png" /> be a conditionally order-complete vector lattice (a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369059.png" />-space). The totality of elements of the form | Finally, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369057.png" /> be a conditionally order-complete vector lattice (a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023690/c02369059.png" />-space). The totality of elements of the form | ||
| Line 22: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Macmillan (1966)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964)</TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Macmillan (1966)</TD></TR> | ||
| + | <TR><TD valign="top">[6]</TD> <TD valign="top"> B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | A conditionally (order-)complete vector lattice is a [[ | + | A conditionally (order-)complete vector lattice is a [[vector lattice]] that is a [[conditionally-complete lattice]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Köthe, "Topological vector spaces" , '''1''' , Springer (1969)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , '''I''' , North-Holland (1971)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Köthe, "Topological vector spaces" , '''1''' , Springer (1969)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , '''I''' , North-Holland (1971)</TD></TR> | ||
| + | </table> | ||
Revision as of 19:42, 8 December 2014
An operation which brings a subset $M$ of a given set $X$ into correspondence with another subset $N$ so that if $M$ and $N$ are known, it is possible in some way to reproduce $X$. Depending on the structure with which $X$ is endowed, one distinguishes various definitions of complementation, as well as various methods of reconstituting $X$ from $M$ and $N$.
Sets
In the general theory of sets the complement of a subset $M$ (or complementary subset, relative complement) in a set $X$ is the subset $\complement_X M$ (or $\complement M$ if $X$ is assumed, or $X \setminus M$) consisting of all elements $x \in X$ not belonging to $M$; an important property is the duality principle (one of the De Morgan laws): $$ \complement \bigcup_{\xi} M_\xi = \bigcap_\xi \complement M_\xi $$
Linear spaces
Let $X$ have a structure of a linear space and let $M$ be a subspace of $X$. A subspace $N \subset X$ is said to be a direct algebraic complement (or algebraic complement, for short) of $M$ if any $x \in X$ can be uniquely represented as $x = y+z$, $y \in M$, $z \in N$. This is equivalent to the conditions $X = M + N$; $M \cap N = \{0\}$. Any subspace of $X$ has an algebraic complement, but this complement is not uniquely determined.
Linear topological spaces
Let 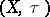 be a linear topological space and let
be a linear topological space and let 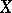 be the direct algebraic sum
be the direct algebraic sum 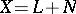 of its subspaces
of its subspaces 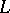 and
and 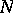 , regarded as linear topological spaces with the induced topology. The one-to-one mapping
, regarded as linear topological spaces with the induced topology. The one-to-one mapping 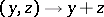 of the Cartesian product
of the Cartesian product 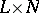 onto
onto 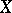 , which is continuous by virtue of the linearity of the topology
, which is continuous by virtue of the linearity of the topology  , does not have, in general, a continuous inverse. If this mapping is a homeomorphism, i.e. if
, does not have, in general, a continuous inverse. If this mapping is a homeomorphism, i.e. if 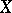 is the direct topological sum of the spaces
is the direct topological sum of the spaces 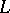 and
and 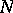 , the subspace
, the subspace 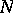 is said to be the direct topological complement of the subspace
is said to be the direct topological complement of the subspace 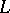 , the latter being known as a complementable subspace. Not all subspaces in an arbitrary linear topological space, not even the finite-dimensional ones, are complementable. The following necessary and sufficient condition for complementability holds: The subspace
, the latter being known as a complementable subspace. Not all subspaces in an arbitrary linear topological space, not even the finite-dimensional ones, are complementable. The following necessary and sufficient condition for complementability holds: The subspace 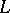 is topologically isomorphic to
is topologically isomorphic to 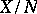 , where
, where 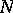 is an algebraic complement of
is an algebraic complement of 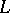 . This criterion entails the following sufficient conditions for complementability:
. This criterion entails the following sufficient conditions for complementability: 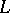 is closed and has finite codimension;
is closed and has finite codimension; 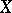 is locally convex and
is locally convex and 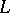 is finite-dimensional; etc.
is finite-dimensional; etc.
Hilbert spaces
A special case of topological complementation is the orthogonal complement of a subspace 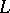 of a Hilbert space
of a Hilbert space 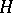 . This is the set
. This is the set
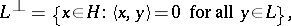 |
which is a closed subspace of 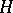 . An important fact in the theory of Hilbert spaces is that any closed subspace of a Hilbert space has an orthogonal complement,
. An important fact in the theory of Hilbert spaces is that any closed subspace of a Hilbert space has an orthogonal complement, 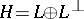 .
.
Vector lattices
Finally, let 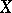 be a conditionally order-complete vector lattice (a
be a conditionally order-complete vector lattice (a  -space). The totality of elements of the form
-space). The totality of elements of the form
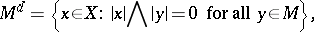 |
which is a linear subspace of  , is said to be the disjoint complement of the set
, is said to be the disjoint complement of the set  . If
. If  is a linear subspace, then, in the general case,
is a linear subspace, then, in the general case, 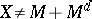 , but if
, but if 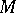 is a component (also known as a band or an order-complete ideal), i.e. a linear subspace such that
is a component (also known as a band or an order-complete ideal), i.e. a linear subspace such that 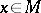 and
and 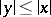 imply that
imply that 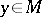 , and such that
, and such that  is closed with respect to least upper and greatest lower bounds, then
is closed with respect to least upper and greatest lower bounds, then 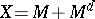 (the set
(the set 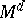 is a component for any
is a component for any 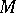 ;
; 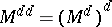 is the smallest component containing the set
is the smallest component containing the set 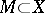 ).
).
References
| [1] | N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) |
| [3] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [4] | A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) |
| [5] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) |
| [6] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian) |
Comments
A conditionally (order-)complete vector lattice is a vector lattice that is a conditionally-complete lattice.
References
| [a1] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) |
| [a2] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
Complementation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complementation&oldid=35505