Difference between revisions of "Minkowski theorem"
(Importing text file) |
(Category:Number theory) |
||
| Line 1: | Line 1: | ||
| − | Minkowski's theorem on convex bodies is the most important theorem in the geometry of numbers, and is the basis for the existence of the [[Geometry of numbers|geometry of numbers]] as a separate division of number theory. It was established by H. Minkowski in 1896 (see [[#References|[1]]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640901.png" /> be a closed convex body, symmetric with respect to the origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640902.png" /> and having volume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640903.png" />. Then every point lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640904.png" /> of determinant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640905.png" /> for which | + | Minkowski's theorem on convex bodies is the most important theorem in the geometry of numbers, and is the basis for the existence of the [[Geometry of numbers|geometry of numbers]] as a separate division of number theory. It was established by H. Minkowski in 1896 (see [[#References|[1]]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640901.png" /> be a closed convex body, symmetric with respect to the origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640902.png" /> and having volume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640903.png" />. Then every [[Lattice of points|point lattice]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640904.png" /> of determinant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640905.png" /> for which |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640906.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064090/m0640906.png" /></td> </tr></table> | ||
| Line 35: | Line 35: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)</TD></TR></table> | ||
| + | |||
| + | [[Category:Number theory]] | ||
Revision as of 19:14, 15 November 2014
Minkowski's theorem on convex bodies is the most important theorem in the geometry of numbers, and is the basis for the existence of the geometry of numbers as a separate division of number theory. It was established by H. Minkowski in 1896 (see [1]). Let 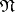 be a closed convex body, symmetric with respect to the origin
be a closed convex body, symmetric with respect to the origin  and having volume
and having volume 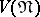 . Then every point lattice
. Then every point lattice 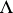 of determinant
of determinant  for which
for which
 |
has a point in  distinct from
distinct from  .
.
An equivalent formulation of Minkowski's theorem is:
 |
where  is the critical determinant of the body
is the critical determinant of the body 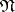 (see Geometry of numbers). A generalization of Minkowski's theorem to non-convex bodies is Blichfeldt's theorem (see Geometry of numbers). The theorems of Minkowski and Blichfeldt enable one to estimate from above the arithmetic minima of distance functions.
(see Geometry of numbers). A generalization of Minkowski's theorem to non-convex bodies is Blichfeldt's theorem (see Geometry of numbers). The theorems of Minkowski and Blichfeldt enable one to estimate from above the arithmetic minima of distance functions.
References
| [1] | H. Minkowski, "Geometrie der Zahlen" , Chelsea, reprint (1953) |
Comments
A refinement of Minkowski's theorem employing Fourier series was given by C.L. Siegel. A different refinement is Minkowski's theorem on successive minima (see Geometry of numbers). These refinements have applications in algebraic number theory and in Diophantine approximation. For a collection of other conditions which guarantee the existence of lattice points in a convex body see .
Minkowski's theorem on linear forms: The system of inequalities
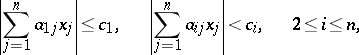 |
where  are real numbers, has an integer solution
are real numbers, has an integer solution  if
if  . This was established by H. Minkowski in 1896 (see [1]). Minkowski's theorem on linear forms is a corollary of the more general theorem of Minkowski on a convex body (see part 1).
. This was established by H. Minkowski in 1896 (see [1]). Minkowski's theorem on linear forms is a corollary of the more general theorem of Minkowski on a convex body (see part 1).
References
| [1] | H. Minkowski, "Geometrie der Zahlen" , Chelsea, reprint (1953) |
| [2] | H. Minkowski, "Diophantische Approximationen" , Chelsea, reprint (1957) |
| [3] | J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1972) |
E.I. Kovalevskaya
Comments
The problem when the first inequality in Minkowski's theorem on linear forms can be replaced by strict inequality was solved by G. Hajós.
References
| [a1] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) |
| [a2] | P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) |
Minkowski theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minkowski_theorem&oldid=34527