Difference between revisions of "Jordan matrix"
(also Jordan canonical form, Jordan normal form) |
m (link) |
||
| Line 11: | Line 11: | ||
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543407.png" />. The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543408.png" /> is called the Jordan block of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434010.png" /> with eigen value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434011.png" />. Every block is defined by an elementary divisor (cf. [[Elementary divisors|Elementary divisors]], see [[#References|[5]]]). | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543407.png" />. The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543408.png" /> is called the Jordan block of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434010.png" /> with eigen value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434011.png" />. Every block is defined by an elementary divisor (cf. [[Elementary divisors|Elementary divisors]], see [[#References|[5]]]). | ||
| − | For an arbitrary square matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434012.png" /> over an algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434013.png" /> there always exists a square non-singular matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434014.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434015.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434016.png" /> is a Jordan matrix (in other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434017.png" /> is similar over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434018.png" /> to a Jordan matrix). This assertion is valid under weaker restrictions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434019.png" />: For a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434020.png" /> to be similar to a Jordan matrix it is necessary and sufficient that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434021.png" /> contains all roots of the minimum polynomial of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434022.png" />. The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434023.png" /> mentioned above is called a Jordan form (or Jordan normal form) of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434024.png" />. C. Jordan [[#References|[1]]] was one of the first to consider such a normal form (see also the historical survey in Chapts. VI and VII of [[#References|[2]]]). | + | For an arbitrary square matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434012.png" /> over an algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434013.png" /> there always exists a square non-singular matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434014.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434015.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434016.png" /> is a Jordan matrix (in other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434017.png" /> is [[Similar matrices|similar]] over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434018.png" /> to a Jordan matrix). This assertion is valid under weaker restrictions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434019.png" />: For a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434020.png" /> to be similar to a Jordan matrix it is necessary and sufficient that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434021.png" /> contains all roots of the minimum polynomial of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434022.png" />. The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434023.png" /> mentioned above is called a Jordan form (or Jordan normal form) of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434024.png" />. C. Jordan [[#References|[1]]] was one of the first to consider such a normal form (see also the historical survey in Chapts. VI and VII of [[#References|[2]]]). |
The Jordan form of a matrix is not uniquely determined, but only up to the order of the Jordan blocks. More exactly, two Jordan matrices are similar over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434025.png" /> if and only if they consist of the same Jordan blocks and differ only in the distribution of the blocks along the main diagonal. The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434026.png" /> of Jordan blocks of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434027.png" /> with eigen value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434028.png" /> in a Jordan form of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434029.png" /> is given by the formula | The Jordan form of a matrix is not uniquely determined, but only up to the order of the Jordan blocks. More exactly, two Jordan matrices are similar over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434025.png" /> if and only if they consist of the same Jordan blocks and differ only in the distribution of the blocks along the main diagonal. The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434026.png" /> of Jordan blocks of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434027.png" /> with eigen value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434028.png" /> in a Jordan form of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434029.png" /> is given by the formula | ||
Revision as of 20:41, 16 October 2014
also Jordan canonical form, Jordan normal form
A square block-diagonal matrix  over a field
over a field 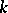 of the form
of the form
 |
where  is a square matrix of order
is a square matrix of order 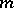 of the form
of the form
 |
 . The matrix
. The matrix 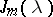 is called the Jordan block of order
is called the Jordan block of order 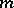 with eigen value
with eigen value 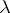 . Every block is defined by an elementary divisor (cf. Elementary divisors, see [5]).
. Every block is defined by an elementary divisor (cf. Elementary divisors, see [5]).
For an arbitrary square matrix 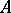 over an algebraically closed field
over an algebraically closed field 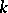 there always exists a square non-singular matrix
there always exists a square non-singular matrix 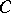 over
over 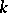 such that
such that 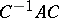 is a Jordan matrix (in other words,
is a Jordan matrix (in other words, 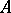 is similar over
is similar over 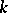 to a Jordan matrix). This assertion is valid under weaker restrictions on
to a Jordan matrix). This assertion is valid under weaker restrictions on  : For a matrix
: For a matrix 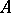 to be similar to a Jordan matrix it is necessary and sufficient that
to be similar to a Jordan matrix it is necessary and sufficient that 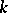 contains all roots of the minimum polynomial of
contains all roots of the minimum polynomial of  . The matrix
. The matrix 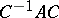 mentioned above is called a Jordan form (or Jordan normal form) of the matrix
mentioned above is called a Jordan form (or Jordan normal form) of the matrix  . C. Jordan [1] was one of the first to consider such a normal form (see also the historical survey in Chapts. VI and VII of [2]).
. C. Jordan [1] was one of the first to consider such a normal form (see also the historical survey in Chapts. VI and VII of [2]).
The Jordan form of a matrix is not uniquely determined, but only up to the order of the Jordan blocks. More exactly, two Jordan matrices are similar over 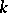 if and only if they consist of the same Jordan blocks and differ only in the distribution of the blocks along the main diagonal. The number
if and only if they consist of the same Jordan blocks and differ only in the distribution of the blocks along the main diagonal. The number 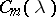 of Jordan blocks of order
of Jordan blocks of order 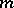 with eigen value
with eigen value  in a Jordan form of a matrix
in a Jordan form of a matrix 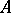 is given by the formula
is given by the formula
 |
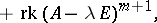 |
where  is the unit matrix of the same order
is the unit matrix of the same order  as
as 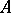 ,
, 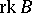 is the rank of the matrix
is the rank of the matrix 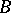 , and
, and 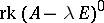 is
is  , by definition.
, by definition.
There are other types of normal forms of matrices besides a Jordan normal form. They are resorted to, for example, when it is desired to avoid the non-uniqueness of the reduction to a Jordan normal form, or when the ground field does not contain all roots of the minimum polynomial of the matrix (see [2]–[5]).
From the point of view of the theory of invariants, a Jordan matrix is a canonical representative in the orbits of the adjoint representation of the general linear group. The determination of analogous representatives for an arbitrary reductive algebraic group is still (1978) not completely solved (see [6]–[7]).
References
| [1] | C. Jordan, "Traité des substitutions et des équations algébriques" , Paris (1870) pp. 114–125 MR1188877 MR0091260 Zbl 03.0042.02 |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) MR0643362 Zbl 1139.12001 |
| [3] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [4] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [5] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) Zbl 0396.15001 |
| [6] | A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970) Zbl 0192.36201 |
| [7] | R. Steinberg, "Classes of elements of semisimple algebraic groups" , Internat. Congress Mathematicians (Moscow, 1966) , Mir (1968) pp. 277–283 MR0238856 Zbl 0192.36202 |
Jordan matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_matrix&oldid=33699