Difference between revisions of "Sharing"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''imputation (in the theory of games)'' | ''imputation (in the theory of games)'' | ||
| − | A distribution of the overall gain of all players in a [[Cooperative game|cooperative game]] which satisfies the rationality condition. Formally, if for a game with a set | + | A distribution of the overall gain of all players in a [[Cooperative game|cooperative game]] which satisfies the rationality condition. Formally, if for a game with a set $J=\{1,\ldots,n\}$ of players a characteristic function $v(J)$ is defined, a sharing is a vector $x=(x_1,\ldots,x_n)$ such that $\sum_{i=1}^n$; $x_i\geq v(i)$, $i=1,\ldots,n$. |
Revision as of 13:27, 9 August 2014
imputation (in the theory of games)
A distribution of the overall gain of all players in a cooperative game which satisfies the rationality condition. Formally, if for a game with a set $J=\{1,\ldots,n\}$ of players a characteristic function $v(J)$ is defined, a sharing is a vector $x=(x_1,\ldots,x_n)$ such that $\sum_{i=1}^n$; $x_i\geq v(i)$, $i=1,\ldots,n$.
Comments
References
| [a1] | A. Rapoport, "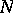 -person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 92; 97–100 |
How to Cite This Entry:
Sharing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sharing&oldid=32780
Sharing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sharing&oldid=32780
This article was adapted from an original article by G.N. Dyubin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article