Difference between revisions of "Epicycloid"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are: | A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are: | ||
| − | + | $$x=(r+R)\cos\theta-r\cos\left[(r+R)\frac\theta r\right],$$ | |
| − | + | $$y=(r+R)\sin\theta-r\sin\left[(r+R)\frac\theta r\right],$$ | |
| − | where | + | where $r$ is the radius of the rolling and $R$ that of the fixed circle, and $\theta$ is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the $x$-axis. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860a.gif" /> | ||
| Line 11: | Line 12: | ||
Figure: e035860a | Figure: e035860a | ||
| − | + | $m=3$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860b.gif" /> | ||
| Line 17: | Line 18: | ||
Figure: e035860b | Figure: e035860b | ||
| − | + | $m=3/2$ | |
| − | Depending on the value of the modulus | + | Depending on the value of the modulus $m=R/r$, the resulting epicycloid has different forms. For $m=1$ it is a cardioid, and if $m$ is an integer, the curve consists of $m$ distinct branches. The cusps $A_1,\ldots,A_m$ have the polar coordinates $\rho=R$, $\phi=\pi2k/m$, $k=0,\ldots,m-1$. The vertices $B_1,\ldots,B_m$ of the curve have the coordinates $\rho=R+2r$, $\phi=\pi(2k+1)/m$. When $m$ is a rational fraction, the branches intersect each other in the interior; when $m$ is irrational there are infinitely many branches and the curve does not return to a point $M$ describing a position obtained previously; for rational $m$ the epicycloid is a closed algebraic curve. The arc length from the point $A_1$ is: |
| − | + | $$s=8Rm(1+m)\sin^2\frac\theta4,$$ | |
| − | and from | + | and from $B_1$ it is |
| − | + | $$s=4Rm(1+m)\cos\frac\theta2.$$ | |
The area of a sector bounded by two radius vectors of the curve and its arc is | The area of a sector bounded by two radius vectors of the curve and its arc is | ||
| − | + | $$S=m\pi(R+mR)(R+2mR).$$ | |
The radius of curvature is | The radius of curvature is | ||
| − | + | $$r_k=\frac{4Rm(1+m)}{2m+1}\sin\frac\theta2.$$ | |
When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or epitrochoid (see [[Trochoid|Trochoid]]). Epicycloids belong to the so-called cycloidal curves (cf. [[Cycloidal curve|Cycloidal curve]]). | When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or epitrochoid (see [[Trochoid|Trochoid]]). Epicycloids belong to the so-called cycloidal curves (cf. [[Cycloidal curve|Cycloidal curve]]). | ||
Revision as of 10:40, 7 August 2014
A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are:
$$x=(r+R)\cos\theta-r\cos\left[(r+R)\frac\theta r\right],$$
$$y=(r+R)\sin\theta-r\sin\left[(r+R)\frac\theta r\right],$$
where $r$ is the radius of the rolling and $R$ that of the fixed circle, and $\theta$ is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the $x$-axis.
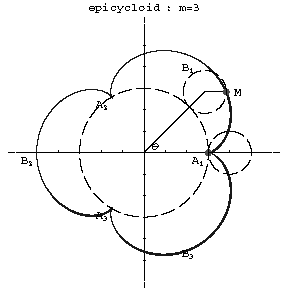
Figure: e035860a
$m=3$

Figure: e035860b
$m=3/2$
Depending on the value of the modulus $m=R/r$, the resulting epicycloid has different forms. For $m=1$ it is a cardioid, and if $m$ is an integer, the curve consists of $m$ distinct branches. The cusps $A_1,\ldots,A_m$ have the polar coordinates $\rho=R$, $\phi=\pi2k/m$, $k=0,\ldots,m-1$. The vertices $B_1,\ldots,B_m$ of the curve have the coordinates $\rho=R+2r$, $\phi=\pi(2k+1)/m$. When $m$ is a rational fraction, the branches intersect each other in the interior; when $m$ is irrational there are infinitely many branches and the curve does not return to a point $M$ describing a position obtained previously; for rational $m$ the epicycloid is a closed algebraic curve. The arc length from the point $A_1$ is:
$$s=8Rm(1+m)\sin^2\frac\theta4,$$
and from $B_1$ it is
$$s=4Rm(1+m)\cos\frac\theta2.$$
The area of a sector bounded by two radius vectors of the curve and its arc is
$$S=m\pi(R+mR)(R+2mR).$$
The radius of curvature is
$$r_k=\frac{4Rm(1+m)}{2m+1}\sin\frac\theta2.$$
When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or epitrochoid (see Trochoid). Epicycloids belong to the so-called cycloidal curves (cf. Cycloidal curve).
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
Epicycloids (and hypocycloids, cf. Hypocycloid) have many equivalent definitions. See, e.g., [a3], pp. 273-277. Epicycloids and, more generally, trochoids are important for kinematical constructions, cf. [a1].
References
| [a1] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a2] | K. Strubecker, "Differential geometry" , I , de Gruyter (1964) |
| [a3] | M. Berger, "Geometry" , I , Springer (1977) |
| [a4] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
Epicycloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epicycloid&oldid=32757