Difference between revisions of "Lindelöf construction"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Lindelof construction to Lindelöf construction over redirect: accented title) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A geometrical construction to find conjugate points in the problem of finding a minimal surface of revolution (see Fig.). | A geometrical construction to find conjugate points in the problem of finding a minimal surface of revolution (see Fig.). | ||
| Line 5: | Line 6: | ||
Figure: l058950a | Figure: l058950a | ||
| − | Lindelöf's construction remains suitable for any variational problem of the simplest type on the | + | Lindelöf's construction remains suitable for any variational problem of the simplest type on the $(x,y)$-plane for which the general integral of the [[Euler equation|Euler equation]] can be represented in the form |
| − | + | $$\frac{y}{c_1}=f\left(\frac{x-c_2}{c_1}\right).$$ | |
| − | The tangents to the extremals at conjugate points | + | The tangents to the extremals at conjugate points $A$ and $A'$ intersect at some point $T$ on the $x$-axis, and the value of the variable integral along the arc $AA'$ is equal to its value on the polygonal line $ATA'$ (see [[#References|[2]]]). An example is the [[Catenoid|catenoid]] with generating curve |
| − | + | $$\frac{y}{c_1}=\cosh\frac{x-c_2}{c_1}.$$ | |
====References==== | ====References==== | ||
Revision as of 17:05, 2 July 2014
A geometrical construction to find conjugate points in the problem of finding a minimal surface of revolution (see Fig.).
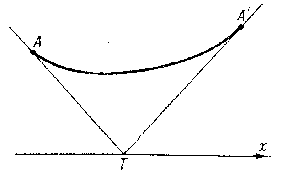
Figure: l058950a
Lindelöf's construction remains suitable for any variational problem of the simplest type on the $(x,y)$-plane for which the general integral of the Euler equation can be represented in the form
$$\frac{y}{c_1}=f\left(\frac{x-c_2}{c_1}\right).$$
The tangents to the extremals at conjugate points $A$ and $A'$ intersect at some point $T$ on the $x$-axis, and the value of the variable integral along the arc $AA'$ is equal to its value on the polygonal line $ATA'$ (see [2]). An example is the catenoid with generating curve
$$\frac{y}{c_1}=\cosh\frac{x-c_2}{c_1}.$$
References
| [1] | E. Lindelöf, "Leçons de calcul des variations" , Paris (1861) |
| [2] | O. Bolza, Bull. Math. Soc. , 18 : 3 (1911) pp. 107–110 |
| [3] | C. Carathéodory, "Variationsrechnung und partielle Differentialgleichungen erster Ordnung" , Teubner (1956) |
Comments
References
| [a1] | A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Blaisdell (1969) |
How to Cite This Entry:
Lindelöf construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_construction&oldid=32354
Lindelöf construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_construction&oldid=32354
This article was adapted from an original article by V.V. Okhrimenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article