|
|
| Line 1: |
Line 1: |
| − | ''at a given point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705401.png" /> of a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705402.png" />'' | + | {{TEX|done}} |
| | + | ''at a given point $M$ of a curve $l$'' |
| | | | |
| − | The circle that has contact of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705403.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705404.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705405.png" /> (see [[Osculation|Osculation]]). If the curvature of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705406.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705407.png" /> is zero, then the osculating circle degenerates into a straight line. The radius of the osculating circle is called the radius of curvature of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705408.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o0705409.png" />, and its centre the centre of curvature (see Fig.). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054010.png" /> is the plane curve given by an equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054011.png" />, then the radius of the osculating circle is given by | + | The circle that has contact of order $n\geq2$ with $l$ at $M$ (see [[Osculation|Osculation]]). If the curvature of $l$ at $M$ is zero, then the osculating circle degenerates into a straight line. The radius of the osculating circle is called the radius of curvature of $l$ at $M$, and its centre the centre of curvature (see Fig.). If $l$ is the plane curve given by an equation $y=f(x)$, then the radius of the osculating circle is given by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054012.png" /></td> </tr></table>
| + | $$\rho=\left|\frac{(1+y'^2)^{3/2}}{y''}\right|.$$ |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o070540a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o070540a.gif" /> |
| Line 9: |
Line 10: |
| | Figure: o070540a | | Figure: o070540a |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054013.png" /> is the spatial curve given by equations | + | If $l$ is the spatial curve given by equations |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054014.png" /></td> </tr></table>
| + | $$x=x(u),\quad y=y(u),\quad z=z(u),$$ |
| | | | |
| | then the radius of the osculating circle is given by | | then the radius of the osculating circle is given by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054015.png" /></td> </tr></table>
| + | $$\rho=\frac{(x'^2+y'^2+z'^2)^{3/2}}{\sqrt{(y'z''-z'y'')^2+(z'x''-x'z'')^2+(x'y''-y'z'')^2}}$$ |
| | | | |
| − | (where the primes denote differentiation with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070540/o07054016.png" />). | + | (where the primes denote differentiation with respect to $u$). |
| | | | |
| | | | |
Revision as of 13:31, 29 April 2014
at a given point $M$ of a curve $l$
The circle that has contact of order $n\geq2$ with $l$ at $M$ (see Osculation). If the curvature of $l$ at $M$ is zero, then the osculating circle degenerates into a straight line. The radius of the osculating circle is called the radius of curvature of $l$ at $M$, and its centre the centre of curvature (see Fig.). If $l$ is the plane curve given by an equation $y=f(x)$, then the radius of the osculating circle is given by
$$\rho=\left|\frac{(1+y'^2)^{3/2}}{y''}\right|.$$
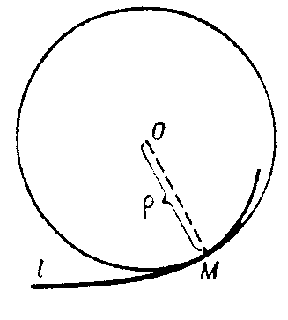
Figure: o070540a
If $l$ is the spatial curve given by equations
$$x=x(u),\quad y=y(u),\quad z=z(u),$$
then the radius of the osculating circle is given by
$$\rho=\frac{(x'^2+y'^2+z'^2)^{3/2}}{\sqrt{(y'z''-z'y'')^2+(z'x''-x'z'')^2+(x'y''-y'z'')^2}}$$
(where the primes denote differentiation with respect to $u$).
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 39 |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 14 |
How to Cite This Entry:
Osculating circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_circle&oldid=31970
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article