Difference between revisions of "Klein interpretation"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A model realizing the system of axioms of [[Lobachevskii geometry|Lobachevskii geometry]]. In the Klein interpretation the Lobachevskii plane is interpreted as the interior of a real non-degenerate absolute quadric on the Euclidean plane. Straight lines of the Lobachevskii plane are realized as chords of the absolute quadric (without end points). Parallels to the straight line | + | {{TEX|done}} |
| + | A model realizing the system of axioms of [[Lobachevskii geometry|Lobachevskii geometry]]. In the Klein interpretation the Lobachevskii plane is interpreted as the interior of a real non-degenerate absolute quadric on the Euclidean plane. Straight lines of the Lobachevskii plane are realized as chords of the absolute quadric (without end points). Parallels to the straight line $MN$ through a point $P$ are realized by the straight lines $PU$ and $PT$ intersecting $MN$ at the points $U$ and $T$ on the absolute quadric (see Fig.). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/k055490a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/k055490a.gif" /> | ||
Latest revision as of 19:31, 17 April 2014
A model realizing the system of axioms of Lobachevskii geometry. In the Klein interpretation the Lobachevskii plane is interpreted as the interior of a real non-degenerate absolute quadric on the Euclidean plane. Straight lines of the Lobachevskii plane are realized as chords of the absolute quadric (without end points). Parallels to the straight line $MN$ through a point $P$ are realized by the straight lines $PU$ and $PT$ intersecting $MN$ at the points $U$ and $T$ on the absolute quadric (see Fig.).
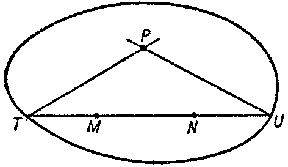
Figure: k055490a
The motions in the Klein interpretation are projective transformations leaving the absolute quadric invariant. The metric quantities are the numerical invariants of the transformations: distances are expressed by means of cross ratios of four points, angles by means of cross ratios of four lines. The absolute quadric can be regarded as the collection of improper points (i.e. pencils of hyperbolic parallels) of the Lobachevskii plane. The Klein interpretation generalizes to the multi-dimensional case.
The Klein interpretation was put forward by F. Klein [1].
References
| [1] | F. Klein, "Ueber die sogenannte Nicht-Euklidische Geometrie" Gött. Nachr. (1871) pp. 419–433 |
| [2] | V.F. Kagan, "Foundations of geometry" , 2 , Moscow-Leningrad (1956) (In Russian) |
| [3] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
| [4] | A.V. Pogorelov, "Foundations of geometry" , Noordhoff (1966) (Translated from Russian) |
Comments
The Klein interpretation is also called the Klein model. See also Poincaré model.
References
| [a1] | A.P. Norden, "Elementare Einführung in die Lobatschewskische Geometrie" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [a2] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1957) |
Klein interpretation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Klein_interpretation&oldid=31838