Difference between revisions of "Hyperbolic functions"
(Importing text file) |
m (TeX encoding is started) |
||
| Line 1: | Line 1: | ||
The functions given by the formulas: | The functions given by the formulas: | ||
| − | + | \begin{equation} | |
| − | + | \sinh x = \frac{e^x-e^{-x}}{2}, | |
| − | + | \end{equation} | |
the hyperbolic sine; and | the hyperbolic sine; and | ||
| − | + | \begin{equation} | |
| − | + | \cosh x = \frac{e^x+e^{-x}}{2}, | |
| − | + | \end{equation} | |
the hyperbolic cosine. The hyperbolic tangent | the hyperbolic cosine. The hyperbolic tangent | ||
| − | + | \begin{equation} | |
| − | + | \tanh x = \frac{\sinh x}{\cosh x}, | |
| − | + | \end{equation} | |
| − | is also sometimes considered. Other notations include: | + | is also sometimes considered. Other notations include: $\operatorname{sh} x$, $\operatorname{Sh} x$, $\operatorname{ch} x$, $\operatorname{Ch} x$, $\operatorname{tgh} x$, $\operatorname{th} x$, $\operatorname{Th} x$. The graphs of these functions are shown in Fig. a. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h048250a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h048250a.gif" /> | ||
Latest revision as of 13:15, 9 December 2012
The functions given by the formulas: \begin{equation} \sinh x = \frac{e^x-e^{-x}}{2}, \end{equation} the hyperbolic sine; and \begin{equation} \cosh x = \frac{e^x+e^{-x}}{2}, \end{equation} the hyperbolic cosine. The hyperbolic tangent \begin{equation} \tanh x = \frac{\sinh x}{\cosh x}, \end{equation} is also sometimes considered. Other notations include: $\operatorname{sh} x$, $\operatorname{Sh} x$, $\operatorname{ch} x$, $\operatorname{Ch} x$, $\operatorname{tgh} x$, $\operatorname{th} x$, $\operatorname{Th} x$. The graphs of these functions are shown in Fig. a.
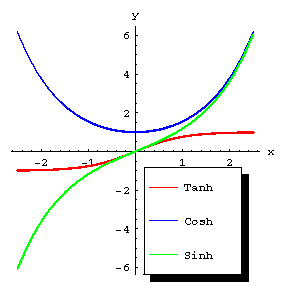
Figure: h048250a
The principal relations are:
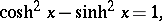 |
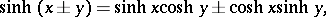 |
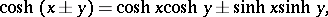 |
 |
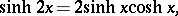 |
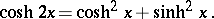 |
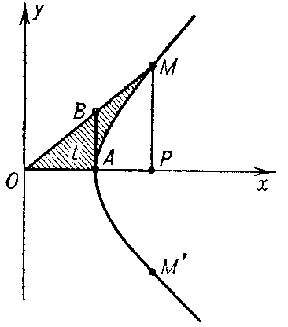
Figure: h048250b
The geometrical interpretation of hyperbolic functions is similar to that of the trigonometric functions (Fig. b). The parametric equations of hyperbolas
 |
make it possible to interpret the abscissa 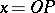 and the ordinate
and the ordinate 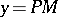 of a point
of a point 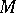 on the equilateral hyperbola
on the equilateral hyperbola 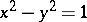 as the hyperbolic sine and cosine; the hyperbolic tangent is the segment
as the hyperbolic sine and cosine; the hyperbolic tangent is the segment 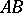 . The parameter
. The parameter 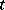 of the point
of the point 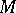 equals twice the area of the sector
equals twice the area of the sector 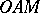 , where
, where 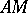 is the arc of the hyperbola. The parameter
is the arc of the hyperbola. The parameter 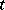 is negative for a point
is negative for a point 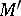 (for
(for 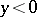 ).
).
The inverse hyperbolic functions are defined by the formulas
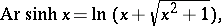 |
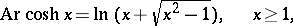 |
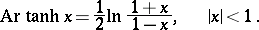 |
The derivatives and basic integrals of the hyperbolic functions are:
 |
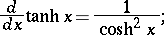 |
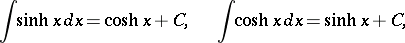 |
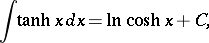 |
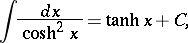 |
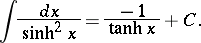 |
The hyperbolic functions 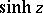 and
and 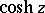 may also be defined by the series
may also be defined by the series
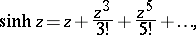 |
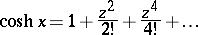 |
in the entire complex  -plane, so that
-plane, so that
 | (3) |
Extensive tabulated values of hyperbolic functions are available. The values of the hyperbolic functions may also be obtained from tables giving 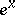 and
and 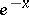 .
.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [2] | , Tables of circular and hyperbolic sines and cosines in radial angle measure , Moscow (1968) (In Russian) |
| [3] | , Tables of 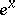 and and 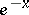 , Moscow (1955) (In Russian) , Moscow (1955) (In Russian) |
Comments
The right-hand sides of the defining relations (1), (2) allow analytic continuation to the whole complex plane. After this, using the Euler formulas one sees that (3) holds, from which the series expansions are readily derived.
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | H.B. Dwight, "Tables of integrals and other mathematical data" , Macmillan (1963) |
Hyperbolic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142