Difference between revisions of "Density of a set"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| + | {{MSC|28A33|49Q15}} | ||
| + | |||
| + | [[Category:Classical measure theory]] | ||
| + | |||
| + | |||
| + | {{TEX|done}} | ||
| + | |||
| + | A concept of classical measure theory generalized further in [[Geometric measure theory]] | ||
| + | |||
| + | ====Lebesgue density of a set==== | ||
| + | Given a Lebesgue measurable set $E$ in the standard Euclidean space $\mathbb R^n$ and a point $x\in\mathbb R^n$, the upper and lower densities of $E$ at $x$ are defined | ||
| + | respectively as | ||
| + | \[ | ||
| + | \limsup_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n} \qquad \mbox{and} \qquad \liminf_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n}\, , | ||
| + | \] | ||
| + | where $\lambda$ denotes the Lebesgue measure and $\omega_n$ the volume of the unit $n$-dimensional ball. If the two numbers coincides, i.e. if the following limit | ||
| + | exists, | ||
| + | \[ | ||
| + | \lim_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n}\, , | ||
| + | \] | ||
| + | the resulting number is called the density of $E$ at $x$. The following is a classical result in measure theory, due to Lebesgue in the case $n=1$: | ||
| + | |||
| + | '''Theorem 1''' | ||
| + | The density of a Lebesgue measurable set $E\subset \mathbb R^n$ is $1$ at $\lambda$--a.e. $x\in E$ and $0$ at $\lambda$--a.e. $x\not \in E$. | ||
| + | |||
| + | ====Density of a measure==== | ||
| + | The concept above has been generalized in geometric measure theory to measures, starting from the work of Besicovitch. Consider a (locally finite) Radon measure $\mu$ in the Euclidean space $\mathbb R^n$, a point $x\in \mathbb R^n$ and a nonnegative real number $\alpha$. The $\alpha$-dimensional upper and lower densities of $\mu$ at $x$ are defined as | ||
| + | \[ | ||
| + | \theta^{\alpha,*} (\mu, x) := \limsup_{r\downarrow 0} \frac{\mu (B_r (x))}{\omega_\alpha r^\alpha} | ||
| + | \qquad \mbox{and}\qquad \theta^\alpha_* (\mu, x) =\liminf_{r\downarrow 0} \frac{\mu (B_r (x))}{\omega_\alpha r^\alpha}\, , | ||
| + | \] | ||
| + | where the normalizing factor $\omega_\alpha$ is the $\alpha$-dimensional volume of the unit ball in $\mathbb R^\alpha$ when $\alpha$ | ||
| + | is a positive integer and in general $\omega_\alpha = \pi^{\alpha/2} \Gamma (1+\alpha/2)$. If the two numbers coincide, the resulting | ||
| + | value is called the $\alpha$-dimensional density of $\mu$ at $x$. The following Theorem by Marstrand shows that the density might | ||
| + | exist and be nontrivial if and only if $\alpha$ is an integer | ||
| + | |||
| + | '''Theorem 2''' | ||
| + | Let $\mu$ be a locally finite Radon measure on $\mathbb R^n$ and $\alpha$ a nonnegative real number such that the $\alpha$-dimensional density of $\mu$ exists and is positive on a set of positibe $\mu$-measure. Then $\alpha$ is necessarily an integer. | ||
| + | |||
| + | ====Lower-dimensional densities of a set==== | ||
| + | Assume $E\subset \mathbb R^n$ is a Borel set with finite $\alpha$-dimensional [[Hausdorff measure]]. The $\alpha$-dimensional upper and lower $\alpha$-dimensional densities $\theta^{\alpha, *} (E, x)$ and $\theta^\alpha_* (E,x)$ of $E$ at $x$ are defined as | ||
| + | \[ | ||
| + | \theta^{\alpha,*} (\mu, x) := \limsup_{r\downarrow 0} \frac{\mathcal{H}^\alpha (E\cap B_r (x))}{\omega_\alpha r^\alpha} | ||
| + | \qquad \mbox{and}\qquad \theta^\alpha_* (\mu, x) =\liminf_{r\downarrow 0} \frac{\mathcal{H}^\alpha (E \cap B_r (x))}{\omega_\alpha r^\alpha}\, . | ||
| + | \] | ||
| + | They correspond, therefore, to the $\alpha$-dimensional densities of the Radon measure $\mu$ given by | ||
| + | \[ | ||
| + | \mu (A) := \mathcal{H}^\alpha (A\cap E)\, . | ||
| + | \] | ||
| + | |||
| + | |||
''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311301.png" /> that is measurable on the real line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311302.png" />, at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311303.png" />'' | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311301.png" /> that is measurable on the real line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311302.png" />, at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031130/d0311303.png" />'' | ||
Revision as of 06:45, 3 August 2012
2020 Mathematics Subject Classification: Primary: 28A33 Secondary: 49Q15 [MSN][ZBL]
A concept of classical measure theory generalized further in Geometric measure theory
Lebesgue density of a set
Given a Lebesgue measurable set $E$ in the standard Euclidean space $\mathbb R^n$ and a point $x\in\mathbb R^n$, the upper and lower densities of $E$ at $x$ are defined respectively as \[ \limsup_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n} \qquad \mbox{and} \qquad \liminf_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n}\, , \] where $\lambda$ denotes the Lebesgue measure and $\omega_n$ the volume of the unit $n$-dimensional ball. If the two numbers coincides, i.e. if the following limit exists, \[ \lim_{r\downarrow 0} \frac{\lambda (B_r (x)\cap E)}{\omega_n r^n}\, , \] the resulting number is called the density of $E$ at $x$. The following is a classical result in measure theory, due to Lebesgue in the case $n=1$:
Theorem 1 The density of a Lebesgue measurable set $E\subset \mathbb R^n$ is $1$ at $\lambda$--a.e. $x\in E$ and $0$ at $\lambda$--a.e. $x\not \in E$.
Density of a measure
The concept above has been generalized in geometric measure theory to measures, starting from the work of Besicovitch. Consider a (locally finite) Radon measure $\mu$ in the Euclidean space $\mathbb R^n$, a point $x\in \mathbb R^n$ and a nonnegative real number $\alpha$. The $\alpha$-dimensional upper and lower densities of $\mu$ at $x$ are defined as \[ \theta^{\alpha,*} (\mu, x) := \limsup_{r\downarrow 0} \frac{\mu (B_r (x))}{\omega_\alpha r^\alpha} \qquad \mbox{and}\qquad \theta^\alpha_* (\mu, x) =\liminf_{r\downarrow 0} \frac{\mu (B_r (x))}{\omega_\alpha r^\alpha}\, , \] where the normalizing factor $\omega_\alpha$ is the $\alpha$-dimensional volume of the unit ball in $\mathbb R^\alpha$ when $\alpha$ is a positive integer and in general $\omega_\alpha = \pi^{\alpha/2} \Gamma (1+\alpha/2)$. If the two numbers coincide, the resulting value is called the $\alpha$-dimensional density of $\mu$ at $x$. The following Theorem by Marstrand shows that the density might exist and be nontrivial if and only if $\alpha$ is an integer
Theorem 2 Let $\mu$ be a locally finite Radon measure on $\mathbb R^n$ and $\alpha$ a nonnegative real number such that the $\alpha$-dimensional density of $\mu$ exists and is positive on a set of positibe $\mu$-measure. Then $\alpha$ is necessarily an integer.
Lower-dimensional densities of a set
Assume $E\subset \mathbb R^n$ is a Borel set with finite $\alpha$-dimensional Hausdorff measure. The $\alpha$-dimensional upper and lower $\alpha$-dimensional densities $\theta^{\alpha, *} (E, x)$ and $\theta^\alpha_* (E,x)$ of $E$ at $x$ are defined as \[ \theta^{\alpha,*} (\mu, x) := \limsup_{r\downarrow 0} \frac{\mathcal{H}^\alpha (E\cap B_r (x))}{\omega_\alpha r^\alpha} \qquad \mbox{and}\qquad \theta^\alpha_* (\mu, x) =\liminf_{r\downarrow 0} \frac{\mathcal{H}^\alpha (E \cap B_r (x))}{\omega_\alpha r^\alpha}\, . \] They correspond, therefore, to the $\alpha$-dimensional densities of the Radon measure $\mu$ given by \[ \mu (A) := \mathcal{H}^\alpha (A\cap E)\, . \]
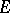 that is measurable on the real line
that is measurable on the real line 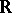 , at a point
, at a point 
The limit (if it exists) of the ratio
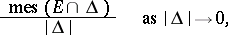 | (1) |
where 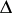 is any segment containing
is any segment containing  and
and 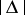 is its length. If one considers an outer measure instead of a measure, one obtains the definition of the outer density of
is its length. If one considers an outer measure instead of a measure, one obtains the definition of the outer density of 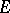 at
at  . Similarly one can introduce the density in
. Similarly one can introduce the density in  -dimensional space. Here the lengths of the segments in
-dimensional space. Here the lengths of the segments in 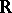 are replaced by the volumes of the corresponding
are replaced by the volumes of the corresponding  -dimensional parallelepipeds with faces parallel to the coordinate planes, while the limit is considered as the diameters of the parallelepipeds tend to zero. For sets from
-dimensional parallelepipeds with faces parallel to the coordinate planes, while the limit is considered as the diameters of the parallelepipeds tend to zero. For sets from 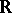 it is useful to employ the concept of the right (left) density of a set
it is useful to employ the concept of the right (left) density of a set 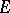 at a point
at a point  , which is obtained from the general definition if in it one considers only segments
, which is obtained from the general definition if in it one considers only segments 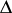 having left (right) ends at
having left (right) ends at  . Very often, the concept of density is used when the density of the set is equal to one (see Density point) or zero (see Thinness of a set).
. Very often, the concept of density is used when the density of the set is equal to one (see Density point) or zero (see Thinness of a set).
References
| [1] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Comments
See [a1] for a nice topological application of these notions.
References
| [a1] | F.D. Tall, "The density topology" Pacific J. Math , 62 (1976) pp. 275–284 |
Density of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_of_a_set&oldid=27339