Difference between revisions of "Sobolev space"
(Starting LaTeX encoding of this article) |
|||
| Line 8: | Line 8: | ||
The norm of a function $f\in W^l_p(\Omega)$ is given by | The norm of a function $f\in W^l_p(\Omega)$ is given by | ||
| − | \begin{equation | + | \begin{equation}\label{eq:1} |
\lVert f\rVert_{W^l_p(\Omega)}=\sum_{\lvert k\rvert\leq l} | \lVert f\rVert_{W^l_p(\Omega)}=\sum_{\lvert k\rvert\leq l} | ||
\lVert f^{(k)}\rVert_{L_p(\Omega)}. | \lVert f^{(k)}\rVert_{L_p(\Omega)}. | ||
| − | \end{equation | + | \end{equation} |
Here | Here | ||
\begin{equation*} | \begin{equation*} | ||
| Line 39: | Line 39: | ||
<!-- END CODE TO BE REMOVED ---> | <!-- END CODE TO BE REMOVED ---> | ||
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598014.png" />, this norm is equal to the essential supremum: | + | When $p=\infty$, this norm is equal to the essential supremum: |
| + | \begin{equation*} | ||
| + | \lVert \psi\rVert_{L_\infty(\Omega)} | ||
| + | =\operatorname*{ess sup}_{x\in\Omega}\lvert\psi(x)\rvert \qquad (p=\infty), | ||
| + | \end{equation*} | ||
| + | that is, to the greatest lower bound of the set of all $A$ for which $A<\lvert\psi(x)\rvert$ on a set of measure zero. | ||
| + | |||
| + | <!-- BEGIN CODE TO BE REMOVED ---> | ||
| + | <!-- When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598014.png" />, this norm is equal to the essential supremum: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598015.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598015.png" /></td> </tr></table> | ||
| − | that is, to the greatest lower bound of the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598016.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598017.png" /> on a set of measure zero. | + | that is, to the greatest lower bound of the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598016.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598017.png" /> on a set of measure zero. --> |
| + | <!-- END CODE TO BE REMOVED ---> | ||
| − | The space | + | The space $W^l_p(\Omega)$ was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [[#References|[1]]], [[#References|[2]]]). |
Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a [[Banach space|Banach space]]. | Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a [[Banach space|Banach space]]. | ||
| − | < | + | <!-- BEGIN CODE TO BE REMOVED ---> |
| + | <!-- The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598018.png" /> was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [[#References|[1]]], [[#References|[2]]]). | ||
| + | |||
| + | Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a [[Banach space|Banach space]]. ---> | ||
| + | <!-- END CODE TO BE REMOVED ---> | ||
| − | It is sometimes convenient to replace the expression (1) for the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598033.png" /> by the following: | + | $W^l_p(\Omega)$ is considered in conjunction with the linear subspace |
| + | $W^l_{pc}(\Omega)$ consisting of functions having partial derivatives of order $l$ that are uniformly continuous on $\Omega$. $W^l_{pc}(\Omega)$ has advantages over $W^l_p(\Omega)$, although it is not closed in the metric of $W^l_p(\Omega)$ and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space $W^l_{pc}(\Omega)$ is dense in $W^l_p(\Omega)$ for all $p$, $1\leq p<\infty$, that is, for such domains the space $W^l_p(\Omega)$ acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of $W^l_p(\Omega)$ by functions from $W^l_{pc}(\Omega)$. | ||
| + | |||
| + | <!-- BEGIN CODE TO BE REMOVED ---> | ||
| + | <!-- <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598019.png" /> is considered in conjunction with the linear subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598020.png" /> consisting of functions having partial derivatives of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598021.png" /> that are uniformly continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598022.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598023.png" /> has advantages over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598024.png" />, although it is not closed in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598025.png" /> and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598026.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598027.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598029.png" />, that is, for such domains the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598030.png" /> acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598031.png" /> by functions from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598032.png" />. ---> | ||
| + | <!-- END CODE TO BE REMOVED ---> | ||
| + | |||
| + | It is sometimes convenient to replace the expression \eqref{eq:1} for the norm of | ||
| + | $f\in W^l_p(\Omega)$ by the following: | ||
| + | \begin{equation}\label{eq:2} | ||
| + | \lVert f\rVert^\prime_{W^l_p(\Omega)}=\left( \int_\Omega | ||
| + | \sum_{\lvert k\rvert\leq l} \lvert f^{(k)}(x)\rvert^p \,dx \right)^{1/p} | ||
| + | \qquad (1\leq p<\infty). | ||
| + | \end{equation} | ||
| + | The norm \eqref{eq:2} is equivalent to the norm \eqref{eq:1}, i.e. | ||
| + | $c_1 \lVert f\rVert \leq \lVert f\rVert^\prime \leq c_2 \lVert f\rVert$, | ||
| + | where $c_1, c_2>0$ do not depend on $f$. When $p=2$, \eqref{eq:2} is a Hilbert norm, and this fact is widely used in applications. | ||
| + | |||
| + | <!-- BEGIN CODE TO BE REMOVED ---> | ||
| + | <!-- It is sometimes convenient to replace the expression (1) for the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598033.png" /> by the following: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1prm)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1prm)</td></tr></table> | ||
| Line 57: | Line 89: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598035.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598035.png" /></td> </tr></table> | ||
| − | The norm (1prm) is equivalent to the norm (1) i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598036.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598037.png" /> do not depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598038.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598039.png" />, (1prm) is a Hilbert norm, and this fact is widely used in applications. | + | The norm (1prm) is equivalent to the norm (1) i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598036.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598037.png" /> do not depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598038.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598039.png" />, (1prm) is a Hilbert norm, and this fact is widely used in applications. ---> |
| + | <!-- END CODE TO BE REMOVED ---> | ||
| + | |||
The boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598040.png" /> of a bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598041.png" /> is said to be Lipschitz if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598042.png" /> there is a rectangular coordinate system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598043.png" /> with origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598044.png" /> so that the box | The boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598040.png" /> of a bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598041.png" /> is said to be Lipschitz if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598042.png" /> there is a rectangular coordinate system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598043.png" /> with origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085980/s08598044.png" /> so that the box | ||
Revision as of 22:25, 3 May 2012
A space $W^l_p(\Omega)$ of functions $f=f(x)=f(x_1,\ldots,x_n)$ on a set $\Omega\subset\RR^n$ (usually open) such that the $p$-th power of the absolute value of $f$ and of its generalized derivatives (cf. Generalized derivative) up to and including order $l$ are integrable ($1\leq p\leq \infty$).
The norm of a function $f\in W^l_p(\Omega)$ is given by
\begin{equation}\label{eq:1}
\lVert f\rVert_{W^l_p(\Omega)}=\sum_{\lvert k\rvert\leq l}
\lVert f^{(k)}\rVert_{L_p(\Omega)}.
\end{equation}
Here
\begin{equation*}
f^{(k)}=\frac{\partial^{\lvert k\rvert}f}{\partial x_1^{k_1}\cdots
\partial x_n^{k_n}},\qquad f^{(0)}=f,
\end{equation*}
is the generalized partial derivative of $f$ of order
$\lvert k\rvert=\sum_{j=1}^n k_j$, and
\begin{equation*}
\lVert \psi\rVert_{L_p(\Omega)}
=\left( \int_\Omega \lvert\psi(x)\rvert^p\,dx \right)^{1/p}
\qquad (1\leq p\leq \infty).
\end{equation*}
When $p=\infty$, this norm is equal to the essential supremum:
\begin{equation*}
\lVert \psi\rVert_{L_\infty(\Omega)}
=\operatorname*{ess sup}_{x\in\Omega}\lvert\psi(x)\rvert \qquad (p=\infty),
\end{equation*}
that is, to the greatest lower bound of the set of all $A$ for which $A<\lvert\psi(x)\rvert$ on a set of measure zero.
The space $W^l_p(\Omega)$ was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [1], [2]).
Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a Banach space.
$W^l_p(\Omega)$ is considered in conjunction with the linear subspace
$W^l_{pc}(\Omega)$ consisting of functions having partial derivatives of order $l$ that are uniformly continuous on $\Omega$. $W^l_{pc}(\Omega)$ has advantages over $W^l_p(\Omega)$, although it is not closed in the metric of $W^l_p(\Omega)$ and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space $W^l_{pc}(\Omega)$ is dense in $W^l_p(\Omega)$ for all $p$, $1\leq p<\infty$, that is, for such domains the space $W^l_p(\Omega)$ acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of $W^l_p(\Omega)$ by functions from $W^l_{pc}(\Omega)$.
It is sometimes convenient to replace the expression \eqref{eq:1} for the norm of
$f\in W^l_p(\Omega)$ by the following:
\begin{equation}\label{eq:2}
\lVert f\rVert^\prime_{W^l_p(\Omega)}=\left( \int_\Omega
\sum_{\lvert k\rvert\leq l} \lvert f^{(k)}(x)\rvert^p \,dx \right)^{1/p}
\qquad (1\leq p<\infty).
\end{equation}
The norm \eqref{eq:2} is equivalent to the norm \eqref{eq:1}, i.e.
$c_1 \lVert f\rVert \leq \lVert f\rVert^\prime \leq c_2 \lVert f\rVert$,
where $c_1, c_2>0$ do not depend on $f$. When $p=2$, \eqref{eq:2} is a Hilbert norm, and this fact is widely used in applications.
The boundary 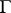 of a bounded domain
of a bounded domain  is said to be Lipschitz if for any
is said to be Lipschitz if for any 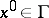 there is a rectangular coordinate system
there is a rectangular coordinate system 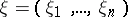 with origin
with origin 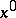 so that the box
so that the box
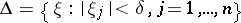 |
is such that the intersection 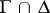 is described by a function
is described by a function 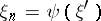 , with
, with
 |
which satisfies on 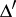 (the projection of
(the projection of 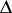 onto the plane
onto the plane 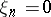 ) the Lipschitz condition
) the Lipschitz condition
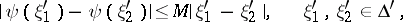 |
where the constant 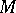 does not depend on the points
does not depend on the points 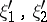 , and
, and  . All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.
. All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.
For a domain with a Lipschitz boundary, (1) is equivalent to the following:
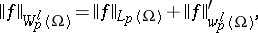 |
where
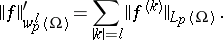 |
One can consider more general anisotropic spaces (classes) 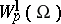 , where
, where 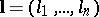 is a positive vector (see Imbedding theorems). For every such vector
is a positive vector (see Imbedding theorems). For every such vector  one can define, effectively and to a known extent exhaustively, a class of domains
one can define, effectively and to a known extent exhaustively, a class of domains 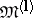 with the property that if
with the property that if 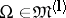 , then any function
, then any function 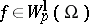 can be extended to
can be extended to 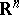 within the same class. More precisely, it is possible to define a function
within the same class. More precisely, it is possible to define a function 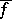 on
on 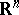 with the properties
with the properties
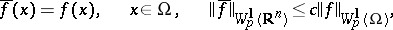 |
where  does not depend on
does not depend on 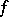 (see [3]).
(see [3]).
In virtue of this property, inequalities of the type found in imbedding theorems for functions 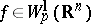 automatically carry over to functions
automatically carry over to functions 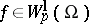 ,
, 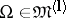 .
.
For vectors 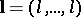 , the domains
, the domains 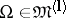 have Lipschitz boundaries, and
have Lipschitz boundaries, and 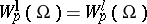 .
.
The investigation of the spaces (classes) 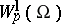 (
(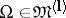 ) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [1], [2]) for an isotropic space
) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [1], [2]) for an isotropic space 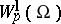 of a domain
of a domain  , star-shaped with respect to some sphere. For the further development of this method see, for example, [3].
, star-shaped with respect to some sphere. For the further development of this method see, for example, [3].
The classes 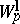 and
and 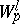 can be generalized to the case of fractional
can be generalized to the case of fractional 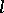 , or vectors
, or vectors 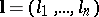 with fractional components
with fractional components 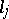 .
.
The space 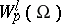 can also be defined for negative integers
can also be defined for negative integers 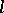 . Its elements are usually generalized functions, that is, linear functionals
. Its elements are usually generalized functions, that is, linear functionals 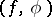 on infinitely-differentiable functions
on infinitely-differentiable functions 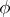 with compact support in
with compact support in  .
.
By definition, a generalized function 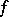 belongs to the class
belongs to the class 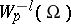 (
(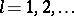 ) if
) if
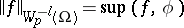 |
is finite, where the supremum is taken over all functions  with norm at most one
with norm at most one 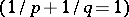 . The functions
. The functions 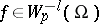 form the space adjoint to the Banach space
form the space adjoint to the Banach space 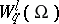 .
.
References
| [1] | S.L. Sobolev, "On a theorem of functional analysis" Transl. Amer. Math. Soc. (2) , 34 (1963) pp. 39–68 Mat. Sb. , 4 (1938) pp. 471–497 |
| [2] | S.L. Sobolev, "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [3] | O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , 1–2 , Wiley (1978) (Translated from Russian) |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
Comments
References
| [a1] | V.G. Maz'ja, "Sobolev spaces" , Springer (1985) |
| [a2] | F. Trèves, "Basic linear partial differential equations" , Acad. Press (1975) pp. Sects. 24–26 |
| [a3] | R.A. Adams, "Sobolev spaces" , Acad. Press (1975) |
Sobolev space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sobolev_space&oldid=25915