Namespaces
Variants
Actions

Difference between revisions of "Genus of a surface"

From Encyclopedia of Mathematics
Jump to: navigation, search
(Importing text file)
 
m (MR/ZBL numbers added)
Line 10: Line 10:
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R., et al. Shafarevich,   "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965)</TD></TR></table>
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R., et al. Shafarevich, "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|1392959}} {{MR|1060325}} {{ZBL|0830.00008}} {{ZBL|0733.14015}} {{ZBL|0832.14026}} {{ZBL|0509.14036}} {{ZBL|0492.14024}} {{ZBL|0379.14006}} {{ZBL|0253.14006}} {{ZBL|0154.21001}} </TD></TR></table>
  
  
Line 18: Line 18:
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne,   "Algebraic geometry" , Springer (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. van de Ven,   "Compact complex surfaces" , Springer (1984)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P.A. Griffiths,   J.E. Harris,   "Principles of algebraic geometry" , Wiley (Interscience) (1978)</TD></TR></table>
+
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. van de Ven, "Compact complex surfaces" , Springer (1984) {{MR|}} {{ZBL|0718.14023}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR></table>

Revision as of 21:52, 30 March 2012

A numerical birational invariant of a two-dimensional algebraic variety defined over an algebraically closed field 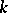. There are two different genera — the arithmetic genus and the geometric genus. The geometric genus 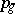of a complete smooth algebraic surface 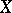is equal to

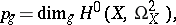i.e. to the dimension of the space of regular differential -forms (cf. Differential form) on 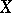. The arithmetic genus 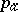of a complete smooth algebraic surface is equal to

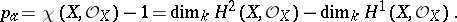The geometric and arithmetic genera of a complete smooth algebraic surface 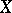are related by the formula 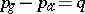, where 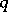is the irregularity of 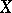, which is equal to the dimension of the space of regular differential 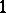-forms on .

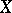References

[1] I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001


Comments

References

[a1] R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001
[a2] A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023
[a3] P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001
How to Cite This Entry:
Genus of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=23843
This article was adapted from an original article by Vik.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=23843"