Kolmogorov-Seliverstov theorem

If the condition

holds with 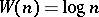, then the Fourier series

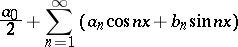converges almost-everywhere. This was established by A.N. Kolmogorov and G.A. Seliverstov (see [1], [2]). In [1] it was actually proved that 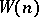can be taken to be 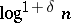for any 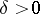, and this statement was strengthened in [2], where its validity was proved for 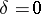as well. This strong form was also obtained by A.I. Plessner [3]. Prior to the Kolmogorov–Seliverstov theorem, the theorem (G.H. Hardy, 1916) was known with . The Kolmogorov–Seliverstov theorem remained the strongest result in this direction until 1966, when the Carleson theorem was proved, according to which one can take 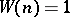. S. Kaczmarz [4] transferred the Kolmogorov–Seliverstov theorem from the trigonometric system to arbitrary orthonormal systems by proving that for the almost-everywhere convergence of series in such systems on some set, one can take for 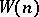a monotone majorant of the Lebesgue function on this set.

References

[1]	A.N. Kolmogorov, G.A. Seliverstov, "Sur la convergence des séries de Fourier" C.R. Acad. Sci. Paris , 178 (1924) pp. 303–306
[2]	A.N. Kolmogorov, G.A. Seliverstov, "Sur la convergence des séries de Fourier" Atti Accad. Naz. Lincei , 3 (1926) pp. 307–310
[3]	A.I. Plessner, "Ueber Konvergenz von trigonometrischen Reihen" J. Reine Angew. Math. , 155 (1925) pp. 15–25
[4]	S. Kaczmarz, "Sur la convergence et la sommabilité des développements orthogonaux" Studia Math. , 1 : 1 (1929) pp. 87–121