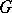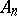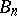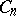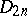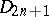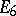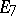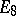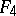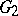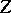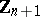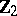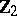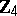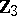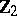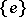Simply-connected group

A topological group (in particular, a Lie group) for which the underlying topological space is simply-connected. The significance of simply-connected groups in the theory of Lie groups is explained by the following theorems.

1) Every connected Lie group is isomorphic to the quotient group of a certain simply-connected group (called the universal covering of ) by a discrete central subgroup isomorphic to .

2) Two simply-connected Lie groups are isomorphic if and only if their Lie algebras are isomorphic; furthermore, every homomorphism of the Lie algebra of a simply-connected group into the Lie algebra of an arbitrary Lie group is the derivation of a (uniquely defined) homomorphism of into .

The centre of a simply-connected semi-simple compact or complex Lie group is finite. It is given in the following table for the various kinds of simple Lie groups.'

<tbody> </tbody>

In the theory of algebraic groups (cf. Algebraic group), a simply-connected group is a connected algebraic group not admitting any non-trivial isogeny 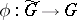, where 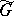is also a connected algebraic group. For semi-simple algebraic groups over the field of complex numbers this definition is equivalent to that given above.

Comments

References

[a1]	G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) MR0207883 Zbl 0131.02702
[a2]	R. Hermann, "Lie groups for physicists" , Benjamin (1966) MR0213463 Zbl 0135.06901
[a3]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 MR0396773 Zbl 0325.20039