Difference between revisions of "Markov chain, periodic"
From Encyclopedia of Mathematics
(Importing text file) |
(MSC|60J10 Category:Markov chains) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60J10}} | ||
| + | |||
| + | [[Category:Markov chains]] | ||
| + | |||
A non-decomposable homogeneous [[Markov chain|Markov chain]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624201.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624202.png" /> in which each state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624203.png" /> has period larger than 1, that is, | A non-decomposable homogeneous [[Markov chain|Markov chain]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624201.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624202.png" /> in which each state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062420/m0624203.png" /> has period larger than 1, that is, | ||
Revision as of 20:24, 9 March 2012
2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]
A non-decomposable homogeneous Markov chain 
, 
in which each state 
has period larger than 1, that is,
 |
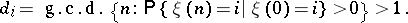In a non-decomposable Markov chain (cf. Markov chain, non-decomposable) all states have the same period. If 
, then the Markov chain is called aperiodic.
Comments
Cf. also Markov chain and Markov chain, decomposable for references.
How to Cite This Entry:
Markov chain, periodic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_periodic&oldid=21654
Markov chain, periodic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_periodic&oldid=21654
This article was adapted from an original article by V.P. Chistyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article