Difference between revisions of "Cramér-von Mises test"
(Importing text file) |
(MSC|62G10 Category:Nonparametric inference) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|62G10}} | ||
| + | |||
| + | [[Category:Nonparametric inference]] | ||
| + | |||
A [[Non-parametric test|non-parametric test]] for testing a hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270101.png" /> which states that independent and identically-distributed random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270102.png" /> have a given continuous distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270103.png" />. The Cramér–von Mises test is based on a statistic of the type | A [[Non-parametric test|non-parametric test]] for testing a hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270101.png" /> which states that independent and identically-distributed random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270102.png" /> have a given continuous distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270103.png" />. The Cramér–von Mises test is based on a statistic of the type | ||
Revision as of 08:34, 8 February 2012
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A non-parametric test for testing a hypothesis  which states that independent and identically-distributed random variables
which states that independent and identically-distributed random variables  have a given continuous distribution function
have a given continuous distribution function  . The Cramér–von Mises test is based on a statistic of the type
. The Cramér–von Mises test is based on a statistic of the type
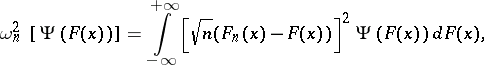 |
where  is the empirical distribution function constructed from the sample
is the empirical distribution function constructed from the sample  and
and  is a certain non-negative function defined on the interval
is a certain non-negative function defined on the interval  such that
such that  ,
, 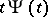 and
and  are integrable on
are integrable on 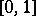 . Tests of this type, based on the "square metric" , were first considered by H. Cramér [1] and R. von Mises [2]. N.V. Smirnov proposed putting
. Tests of this type, based on the "square metric" , were first considered by H. Cramér [1] and R. von Mises [2]. N.V. Smirnov proposed putting 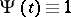 , and showed that in that case, if the hypothesis
, and showed that in that case, if the hypothesis 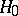 is valid and
is valid and 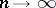 , the statistic
, the statistic 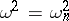 has in the limit an "omega-squared" distribution, independent of the hypothetical distribution function
has in the limit an "omega-squared" distribution, independent of the hypothetical distribution function  . A statistical test for testing
. A statistical test for testing 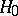 based on the statistic
based on the statistic 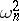 , is called an
, is called an  (Cramér–von Mises–Smirnov) test, and the numerical value of
(Cramér–von Mises–Smirnov) test, and the numerical value of 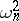 is found using the following representation:
is found using the following representation:
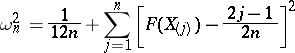 |
where 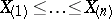 is the variational series based on the sample
is the variational series based on the sample 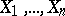 . According to the
. According to the 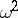 test with significance level
test with significance level 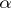 , the hypothesis
, the hypothesis 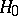 is rejected whenever
is rejected whenever 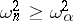 , where
, where 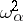 is the upper
is the upper 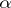 -quantile of the distribution of
-quantile of the distribution of 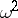 , i.e.
, i.e. 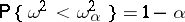 . T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic
. T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic 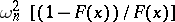 (see [5]).
(see [5]).
References
| [1] | H. Cramér, "Sannolikhetskalkylen och nåcgra av dess användningar" , Stockholm (1926) |
| [2] | R. von Mises, "Mathematical theory of probability and statistics" (1964) (Translated from German) |
| [3] | N.V. Smirnov, "On the 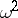 -distribution of von Mises" Mat. Sb. , 2 : 5 (1937) pp. 973–993 (In Russian) (French abstract) -distribution of von Mises" Mat. Sb. , 2 : 5 (1937) pp. 973–993 (In Russian) (French abstract) |
| [4] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [5] | T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness-of-fit" criteria based on stochastic processes" Ann. of Math. Stat. , 23 (1952) pp. 193–212 |
Comments
Usually, the choice 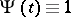 is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of
is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of 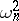 is independent of
is independent of 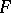 whatever the choice of
whatever the choice of 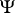 . (The term "square metric" refers to the expression
. (The term "square metric" refers to the expression 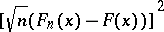 , not to some choice of
, not to some choice of 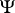 .) Cramér actually considered the test with
.) Cramér actually considered the test with 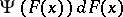 replaced by
replaced by 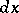 , while von Mises used
, while von Mises used 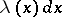 .
.
An alternative to [1] is [a1].
References
| [a1] | H. Cramér, "On the composition of elementary errors II" Skand. Aktuarietidskr. (1928) pp. 171–280 |
Cramér-von Mises test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r-von_Mises_test&oldid=20895