Difference between revisions of "Packing"
(Importing text file) |
(new text added above original text -- cleaning up (merging) to follow) |
||
| Line 1: | Line 1: | ||
| + | == Packing == | ||
| + | |||
| + | A packing of a (finite or infinite) family of sets $M_i$ in a set $A$ is, in its strict sense, | ||
| + | any pairwise disjoint family of subsets $M_i\subset A$. | ||
| + | |||
| + | However, in geometry, the sets $M_i$ are often closed domains, | ||
| + | and then this condition is relaxed to requiring only | ||
| + | that the interiors of the sets are pairwise disjoint. | ||
| + | |||
| + | Lattice packings | ||
| + | |||
| + | As a special case, in vector spaces $V$, such as $\R^d$, | ||
| + | packings of translates $ \{ M+v \mid v \in Z \} $, of a set $ M \subset V $ are considered. | ||
| + | If the set $Z \subset V $ of translation vectors is a lattice, | ||
| + | then the packing is called a lattice packing. | ||
| + | In particular, such packings are investigated in the geometry of numbers and in discrete geometry. | ||
| + | |||
| + | Sphere packings | ||
| + | |||
| + | Packings of congruent spheres are considered both in the geometry of numbers | ||
| + | and in discrete geometry, and have applications in coding theory. | ||
| + | A central problem is finding the densest packing, | ||
| + | and the densest lattice packing, of congruent spheres in $\R^d$. | ||
| + | For $d=3$, the problem (known as Kepler conjecture or Kepler problem) | ||
| + | to decide whether there is a better packing than the densest lattice packing | ||
| + | was a famous open problem that was recently solved by Hales (1998). | ||
| + | With the help of massive computer calculations he showed | ||
| + | that the densest lattice packing of spheres is optimal. | ||
| + | This result is generally considered as correct | ||
| + | but because of its size it has not yet been verified independently. | ||
| + | However, Hales and his team are working on a computer-verifyable version of the proof. | ||
| + | |||
| + | Tilings | ||
| + | |||
| + | A tiling is a packing without gaps, | ||
| + | i.e., such that the $M_i$ are also a covering of $A$. | ||
| + | |||
| + | |||
''of a finite (or infinite) family of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071050/p0710501.png" /> in a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071050/p0710502.png" />'' | ''of a finite (or infinite) family of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071050/p0710501.png" /> in a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071050/p0710502.png" />'' | ||
Revision as of 00:00, 6 February 2012
Packing
A packing of a (finite or infinite) family of sets $M_i$ in a set $A$ is, in its strict sense, any pairwise disjoint family of subsets $M_i\subset A$.
However, in geometry, the sets $M_i$ are often closed domains, and then this condition is relaxed to requiring only that the interiors of the sets are pairwise disjoint.
Lattice packings
As a special case, in vector spaces $V$, such as $\R^d$, packings of translates $ \{ M+v \mid v \in Z \} $, of a set $ M \subset V $ are considered. If the set $Z \subset V $ of translation vectors is a lattice, then the packing is called a lattice packing. In particular, such packings are investigated in the geometry of numbers and in discrete geometry.
Sphere packings
Packings of congruent spheres are considered both in the geometry of numbers and in discrete geometry, and have applications in coding theory. A central problem is finding the densest packing, and the densest lattice packing, of congruent spheres in $\R^d$. For $d=3$, the problem (known as Kepler conjecture or Kepler problem) to decide whether there is a better packing than the densest lattice packing was a famous open problem that was recently solved by Hales (1998). With the help of massive computer calculations he showed that the densest lattice packing of spheres is optimal. This result is generally considered as correct but because of its size it has not yet been verified independently. However, Hales and his team are working on a computer-verifyable version of the proof.
Tilings
A tiling is a packing without gaps, i.e., such that the $M_i$ are also a covering of $A$.
of a finite (or infinite) family of sets 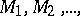 in a set
in a set 
Fulfillment of the conditions
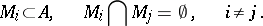 |
In the geometry of numbers usually 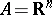 ,
, 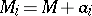 , where
, where 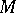 is a given set and the
is a given set and the 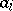 range over a certain set
range over a certain set 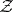 of vectors in
of vectors in  (
(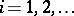 ); in this case one speaks of the packing
); in this case one speaks of the packing 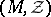 of the set
of the set 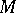 by the system of vectors
by the system of vectors 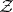 . If
. If 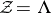 is a point lattice in
is a point lattice in  , one speaks of a lattice packing
, one speaks of a lattice packing 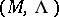 .
.
One also considers packing of sets 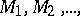 not only in
not only in 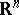 but also in other manifolds, on an
but also in other manifolds, on an  -dimensional sphere, in a given domain, etc. (cf. [1], [2]). Sometimes a packing is defined as a system of (for example, closed domains)
-dimensional sphere, in a given domain, etc. (cf. [1], [2]). Sometimes a packing is defined as a system of (for example, closed domains) 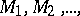 which do not meet in interior points (cf. [1]).
which do not meet in interior points (cf. [1]).
References
| [1] | E.P. Baranovskii, "Packings, coverings, partitions, and certain other distributions in spaces of constant curvature" Progress in Math. , 9 (1971) pp. 209–253 Itogi Nauk. Algebra. Topol. Geom. 1967 (1969) pp. 181–225 |
| [2] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) |
| [3] | C.A. Rogers, "Packing and covering" , Cambridge Univ. Press (1964) |
Comments
Sphere packing has various applications in error-correcting codes (cf. Error-correcting code), the channel coding problem, Steiner systems (cf. Steiner system),  -designs, and in the theory of finite groups. The most important special case is the sphere packing in
-designs, and in the theory of finite groups. The most important special case is the sphere packing in 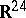 via the Leech lattice. Finite and infinite sphere packing in
via the Leech lattice. Finite and infinite sphere packing in 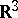 has applications in classical and modern crystallography (cf. Crystallography, mathematical).
has applications in classical and modern crystallography (cf. Crystallography, mathematical).
A packing in 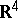 which is also a covering in
which is also a covering in 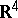 (cf. Covering and packing; Covering (of a set)) is called a tiling or tesselation. In other words: A tiling is a countable family of closed sets which cover
(cf. Covering and packing; Covering (of a set)) is called a tiling or tesselation. In other words: A tiling is a countable family of closed sets which cover 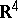 without gaps or overlaps. The sets are called tiles. If all sets are congruent, they are the copies of a prototile.
without gaps or overlaps. The sets are called tiles. If all sets are congruent, they are the copies of a prototile.
In the geometry of numbers, lattice tilings are of interest; there are tilings of the form 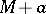 ,
, 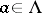 , where
, where 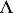 is a lattice of points. For an exhaustive account of planar tilings see [a3]. Higher-dimensional results and, in particular, relations to crystallography are treated in [a2], [a1]. Classical types of tilings are Dirichlet–Voronoi tilings and Delone triangulations or
is a lattice of points. For an exhaustive account of planar tilings see [a3]. Higher-dimensional results and, in particular, relations to crystallography are treated in [a2], [a1]. Classical types of tilings are Dirichlet–Voronoi tilings and Delone triangulations or 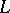 -partitions, see [a1] and Voronoi lattice types.
-partitions, see [a1] and Voronoi lattice types.
References
| [a1] | P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) |
| [a2] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) |
| [a3] | B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1986) |
| [a4] | J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988) |
Packing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Packing&oldid=20852