Difference between revisions of "Cochleoid"
From Encyclopedia of Mathematics
(gather refs) |
m (→References: isbn link) |
||
| Line 15: | Line 15: | ||
====References==== | ====References==== | ||
<table> | <table> | ||
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR> |
| − | <TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) {{ISBN|0-486-60288-5}} {{ZBL|0257.50002}}</TD></TR> |
</table> | </table> | ||
Latest revision as of 20:46, 5 December 2023
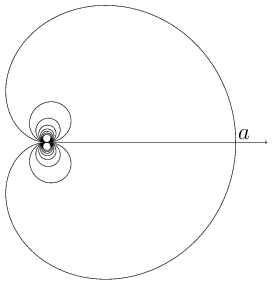
Figure 1. The cochleoid (pdf)
A plane transcendental curve whose equation in polar coordinates is \begin{equation} \rho = a\frac{\sin\varphi}{\varphi}. \end{equation}
The cochleoid has infinitely many spirals, passing through its pole and touching the polar axis (see Fig.). The pole is a singular point of infinite multiplicity. Any straight line through the pole $O$ intersects the cochleoid; the tangents to the cochleoid at these intersection points pass through the same point.
The inverse of the cochleoid with respect to the origin is the quadratrix of Hippias.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 Zbl 0257.50002 |
How to Cite This Entry:
Cochleoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cochleoid&oldid=53707
Cochleoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cochleoid&oldid=53707
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article