Difference between revisions of "Duffin-Schaeffer conjecture"
m (AUTOMATIC EDIT (latexlist): Replaced 93 formulas out of 95 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 95 formulas, 93 were replaced by TEX code.--> | Out of 95 formulas, 93 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Let $f ( q )$ be a function defined on the positive integers and let $\varphi ( q )$ be the Euler [[Totient function|totient function]]. The Duffin–Schaeffer conjecture says that for an arbitrary function $f ( q ) \geq 0$ (zero values are also allowed for $f ( q )$), the Diophantine inequality (cf. also [[Diophantine equations|Diophantine equations]]) | Let $f ( q )$ be a function defined on the positive integers and let $\varphi ( q )$ be the Euler [[Totient function|totient function]]. The Duffin–Schaeffer conjecture says that for an arbitrary function $f ( q ) \geq 0$ (zero values are also allowed for $f ( q )$), the Diophantine inequality (cf. also [[Diophantine equations|Diophantine equations]]) | ||
Revision as of 17:45, 1 July 2020
Let $f ( q )$ be a function defined on the positive integers and let $\varphi ( q )$ be the Euler totient function. The Duffin–Schaeffer conjecture says that for an arbitrary function $f ( q ) \geq 0$ (zero values are also allowed for $f ( q )$), the Diophantine inequality (cf. also Diophantine equations)
\begin{equation} \tag{a1} \left| x - \frac { p } { q } \right| < f ( q ) , \quad \operatorname { gcd } ( p , q ) = 1 , q > 0, \end{equation}
has infinitely many integer solutions $p$ and $q$ for almost-all real $x$ (in the sense of Lebesgue measure) if and only if the series
\begin{equation} \tag{a2} \sum _ { q = 1 } ^ { \infty } \varphi ( q ) f ( q ) \end{equation}
diverges. By the Borel–Cantelli lemma, (a1) has only finitely many solutions for almost-all $x$ if (a2) converges, and by the Gallagher ergodic theorem, the set of all $x \in [ 0,1 ]$ for which (a1) has infinitely many integer solutions has measure either $0$ or $1$.
The Duffin–Schaeffer conjecture is one of the most important unsolved problems in the metric theory of numbers (as of 1998). It was inspired by an effort to replace $f ( q ) = 1 / q ^ { 2 }$ by a smaller function $f ( q )$ for which every irrational number $x$ can be approximated by infinitely many fractions $p / q$ such that (a1) holds. This question was answered by A. Hurwitz in 1891, who showed that the best possible function is $f ( q ) = 1 / ( \sqrt { 5 } q ^ { 2 } )$. The application of Lebesgue measure to improve this $f ( q )$ was made by A. Khintchine [a7] in 1924. He proved that if $q ^ { 2 } f ( q )$ is non-increasing and
\begin{equation} \tag{a3} \sum _ { q = 1 } ^ { \infty } q f ( q ) \end{equation}
diverges, then (a1) has infinitely many integer solutions for almost-all $x$. In 1941, R.J. Duffin and A.C. Schaeffer [a1] improved Khintchine's theorem for $f ( q )$ satisfying $\sum _ { q = 1 } ^ { Q } q f ( q ) \leq c \sum _ { q = 1 } ^ { Q } \varphi ( q ) f ( q )$ for infinitely many $Q$ and some positive constant $c$. They also have given an example of an $f ( q )$ such that (a3) diverges but (a2) converges which naturally leads to the Duffin–Schaeffer conjecture. Up to now (1998), this conjecture remains open. A breakthrough was achieved by P. Erdös [a2], who proved that the conjecture holds, given the additional condition $f ( q ) = c / q ^ { 2 }$ or $f ( q ) = 0$ for some $c > 0$. V.G. Sprindzuk comments in [a11] that the answer may depend upon the Riemann hypothesis (cf. also Riemann hypotheses). He also proposes the following $k$-dimensional analogue of the Duffin–Schaeffer conjecture: There are infinitely many integers $( p _ { 1 } , \dots , p _ { k } )$ and $q$ such that
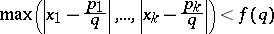 |
and
\begin{equation*} \operatorname { gcd } ( p _ { 1 } \ldots p _ { k } , q ) = 1 \end{equation*}
for almost-all real numbers $( x _ { 1 } , \dots , x _ { k } )$ whenever the series
\begin{equation} \tag{a4} \sum _ { q = 1 } ^ { \infty } ( \varphi ( q ) f ( q ) ) ^ { k } \end{equation}
diverges. A.D. Pollington and R.C. Vaughan [a10] have proved this $k$-dimensional Duffin–Schaeffer conjecture for $k \geq 2$. The corresponding result with $\operatorname { gcd } ( p _ { 1 } , \dots , p _ { k } , q ) = 1$ instead of the condition $\operatorname { gcd } ( p _ { 1 } \ldots p _ { k } , q ) = 1$ was given by P.X. Gallagher [a3].
Various authors have studied the problem that the number of solutions of (a1) with $q \leq N$ is, for almost-all $x$, asymptotically equal to $2\sum _ { q = 1 } ^ { N } \varphi ( q ) f ( q )$.
The problem of restricting both the numerators $p$ and the denominators $q$ in (a1) to sets of number-theoretic interest was investigated by G. Harman. In [a6] he considers (a1) where $p$, $q$ are both prime numbers. In this case, the Duffin–Schaeffer conjecture has the form: If the sum
\begin{equation} \tag{a5} \sum _ { q = 2 , q \text { prime } } ^ { \infty } f ( q ) q ( \operatorname { log } q ) ^ { - 1 } \end{equation}
diverges, then for almost-all $x$ there are infinitely many prime numbers $p$, $q$ which satisfy (a1). Harman has proved this conjecture under certain conditions on $f ( q )$.
A class of sequences $q_n$, $n = 1,2 , \dots$, of distinct positive integers and a class of functions $f ( q ) \geq 0$ is said to satisfy the Duffin–Schaeffer conjecture if the divergence of
\begin{equation} \tag{a6} \sum _ { n = 1 } ^ { \infty } \varphi ( q _ { n } ) f ( q _ { n } ) \end{equation}
implies that for almost-all $x$ there exist infinitely many $n$ such that the Diophantine inequality
\begin{equation*} \left| x - \frac { p } { q_n } \right| < f ( q_n ) \end{equation*}
has an integer solution $p$ that is mutually prime with $q_n$ (cf. also Mutually-prime numbers). There are tree types of results regarding $q_n$, $f ( q )$ satisfying this conjecture (cf. [a5]):
i) any one-to-one sequence $q_n$ and special $f ( q )$ (e.g. $f ( q ) = O ( 1 / q ^ { 2 } )$);
ii) any $f ( q ) \geq 0$ and a special $q_n$ (e.g. $q _ { n } = n ^ { k }$, $k \geq 2$);
iii) special $q_n$, $f ( q )$ (e.g. $f ( q _ { n } ) q _ { n } > c _ { 1 } ( \varphi ( q _ { n } ) / q _ { n } ) ^ { c _ { 2 } }$ for some $c _ { 1 } , c _ { 2 } > 0$). As an interesting consequence of the Erdös result, for almost-all $x$ infinitely many denominators of the continued fraction convergents to $x$ lie in the sequence $q_n$ if and only if (a6) diverges.
Following J. Lesca [a8], one may extend the Duffin–Schaeffer conjecture to the problem of finding sequences $x _ { n } \in [ 0,1 ]$ such that for every non-increasing $y _ { n } \geq 0$, the divergence of
\begin{equation} \tag{a7} \sum _ { n = 1 } ^ { \infty } y _ { n } \end{equation}
implies that for almost-all $x \in [ 0,1 ]$ there exist infinitely many $n$ such that $| x - x _ { n } | < y _ { n }$. These $x _ { n }$ are called eutaxic sequences. This problem encompasses all of the above conjectures.
As an illustration, let $x _ { n }$ be a sequence of reduced fractions with denominators $q_{ m}$, $m = 1,2 , \dots$, and let $y _ { n } = f ( q _ { m } )$ for $x _ { n }$ with a fixed denominator $q_{ m}$. This gives the classical Duffin–Schaeffer conjecture, since (a6) and (a7) coincide. It is known that the sequence of fractional parts $n \, \alpha \, ( \operatorname { mod } 1 )$ is eutaxic if and only if the irrational number $\alpha$ has bounded partial quotients.
Finally, H. Nakada and G. Wagner [a9] have considered a complex version of the Duffin–Schaeffer conjecture for imaginary quadratic number fields.
The basic general reference books are [a11] and [a4].
References
| [a1] | R.J. Duffin, A.C. Schaeffer, "Khintchine's problem in metric diophantine approximation" Duke Math. J. , 8 (1941) pp. 243–255 |
| [a2] | P. Erdös, "On the distribution of convergents of almost all real numbers" J. Number Th. , 2 (1970) pp. 425–441 |
| [a3] | P.X. Gallagher, "Metric simultaneous diophantine approximation II" Mathematika , 12 (1965) pp. 123–127 |
| [a4] | G. Harman, "Metric number theory" , London Math. Soc. Monogr. , 18 , Clarendon Press (1998) |
| [a5] | G. Harman, "Some cases of the Duffin and Schaeffer conjecture" Quart. J. Math. Oxford , 41 : 2 (1990) pp. 395–404 |
| [a6] | G. Harman, "Metric diophantine approximation with two restricted variables III. Two prime numbers" J. Number Th. , 29 (1988) pp. 364–375 |
| [a7] | A. Khintchine, "Einige Saetze über Kettenbruche, mit Anwendungen auf die Theorie der Diophantischen Approximationen" Math. Ann. , 92 (1924) pp. 115–125 |
| [a8] | J. Lesca, "Sur les approximations diophantiennes a'une dimension" Doctoral Thesis Univ. Grenoble (1968) |
| [a9] | H. Nakada, G. Wagner, "Duffin–Schaeffer theorem of diophantine approximation for complex number" Astérisque , 198–200 (1991) pp. 259–263 |
| [a10] | A.D. Pollington, R.C. Vaughan, "The $k$-dimensional Duffin and Schaeffer conjecture" Mathematika , 37 : 2 (1990) pp. 190–200 |
| [a11] | V.G. Sprindzuk, "Metric theory of diophantine approximations" , Winston&Wiley (1979) |
Duffin-Schaeffer conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Duffin-Schaeffer_conjecture&oldid=50487