Difference between revisions of "Inverse scattering, half-axis case"
m (AUTOMATIC EDIT (latexlist): Replaced 193 formulas out of 194 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 194 formulas, 193 were replaced by TEX code.--> | Out of 194 formulas, 193 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
The direct scattering problem on the half-axis consists of finding the solution $u ( x , k )$ to the problem | The direct scattering problem on the half-axis consists of finding the solution $u ( x , k )$ to the problem | ||
Revision as of 17:43, 1 July 2020
The direct scattering problem on the half-axis consists of finding the solution $u ( x , k )$ to the problem
\begin{equation} \tag{a1} u ^ { \prime \prime } + k ^ { 2 } u - q ( x ) u = 0 , x > 0, \end{equation}
\begin{equation} \tag{a2} u ( 0 , k ) = 0 \end{equation}
\begin{equation} \tag{a3} u ( x , k ) = e ^ { i \delta } \operatorname { sin } ( k x + \delta ) + o ( 1 ) , \quad \text { as } x \rightarrow \infty. \end{equation}
Here, $\delta = \delta ( k )$ is to be determined. The function $\delta = \delta ( k )$ is called the phase shift. The coefficient $q ( x )$ is called the scattering potential. It is assumed to be a real-valued function in the class
\begin{equation*} L _ { 1,1 } : = \left\{ q : \int _ { 0 } ^ { \infty } x | q ( x ) | d x < \infty , q = \overline { q } \right\}, \end{equation*}
where the bar stands for complex conjugation. The solution $f ( x , k )$ to (a1) which satisfies the relation $f ( x , k ) = e ^ { i k x } + o ( 1 )$, as $x \rightarrow + \infty$, is called the Jost solution. The function $f ( 0 , k ) : = f ( k )$ is called the Jost function. One has
\begin{equation*} f ( k ) = | f ( k ) | e ^ { - i \delta ( k ) }, \end{equation*}
\begin{equation*} \delta ( - k ) = - \delta ( k ) , k \in \mathbf{R} , \quad \delta ( \infty ) = 0. \end{equation*}
If $q \in L _ { 1 , 1} $, then $f ( x , k )$ exists and is unique, $f ( k )$ is analytic in $\mathbf{C} _ { + } : = \{ k : \operatorname { Im } k > 0 \}$ and has at most finitely many zeros in $\mathbf{C} _ { + }$, all of which are simple and of the form $i k_j$, $k_ j > 0$, $1 \leq j \leq J$. The numbers $- k _ { j } ^ { 2 }$ are the eigenvalues of the self-adjoint operator
\begin{equation*} l : = - \frac { d ^ { 2 } } { d x ^ { 2 } } + q ( x ), \end{equation*}
which is determined by the Dirichlet boundary condition at $x = 0$ in the Hilbert space $L ^ { 2 } ( \mathbf{R} _ { + } )$, $\mathbf{R} _ { + } : = [ 0 , \infty )$ (cf. also Dirichlet boundary conditions). In physics, $- k ^ { 2}j $ are called the bound states. The positive numbers $s _ { j } : = \| f ( x , i k _ { j } ) \| ^ { - 2 _{L ^ { 2} ( \mathbf{R} _ { + } )}}$ are called the norming constants. The function $S ( k ) = f ( - k ) / f ( k ) = e ^ { 2 i \delta ( k ) }$ is called the $S$-matrix (cf. Scattering matrix). The triple 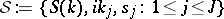 is called the scattering data.
is called the scattering data.
The inverse scattering problem consists of finding $q ( x )$ given $\mathcal{S}$.
The point $k = 0$ can also be a zero of $f ( k )$. It is called a resonance at $k = 0$. If $f ( 0 ) = 0$, then $f ^ { \prime } ( 0 ) \neq 0$. The basic results of inverse scattering theory are (see [a5], [a6]):
1) The uniqueness theorem: $\mathcal{S} \Rightarrow q$; that is, the scattering data determine $q \in L _ { 1 , 1} $ uniquely.
2) The reconstruction theorem: If $\mathcal{S}$, corresponding to a $q \in L _ { 1 , 1} $, is given, then $q ( x )$ can be reconstructed by the Marchenko method, as follows:'
|
3) The characterization theorem: For $\mathcal{S}$ to be the scattering data corresponding to a $q \in L _ { 1 , 1} $ it is necessary and sufficient that the following conditions hold:
i) $\overline { S ( k ) } = S ( - k ) = S ^ { - 1 } ( k )$, $k \in {\bf R}_+$; $S ( \infty ) = 1$, $k_ j > 0$, $s _ { j } > 0$, $1 \leq j \leq J$;
ii) $\operatorname {ind} S ( k ) = - \kappa$, $\kappa = 2 J$ or $\kappa = 2 J + 1$;
iii) $\| F ( x ) \| _ { L^{\infty} ( \mathbf{R} _ { + } ) } + \| F ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } +$
\begin{equation*} + \| x F ^ { \prime } ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } < \infty. \end{equation*}
Here, $\operatorname{ ind } S ( k ) : = ( 1 / 2 \pi ) \int _ { - \infty } ^ { \infty } d \operatorname { ln } S ( k )$.
Note that $\kappa = 2 J$ if $f ( 0 ) \neq 0$, and $\kappa = 2 J + 1$ if $f ( 0 ) = 0$. The mapping $T : q \rightarrow \mathcal{S}$ is a homeomorphism between $L _ { 1 , 1}$ and the space of the scattering data equipped with the norm $\| \mathcal{S} \| : = \int _ { 0 } ^ { \infty } ( 1 + x ) | F ^ { \prime } ( x ) | d x$ (see [a4], [a5] [a6]).
One can prove (see [a6], [a13]) the diagram
\begin{equation*} \delta \Leftrightarrow F \Leftrightarrow A \Leftrightarrow q, \end{equation*}
each step of which is invertible. Here, $F = F ( x )$ and $A = A ( x , y )$ are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that $q \in L _ { 1 , 1} $ or $\mathcal{S}$ satisfies the characterization conditions).
Other methods for solving the inverse scattering problem on the half-axis are based on the solution of the inverse problem of recovery of $q ( x )$ from the spectral function $\rho : = \rho ( \lambda )$ ($\mathcal{S} \Rightarrow \rho \Rightarrow q$) and the Krein method ([a1], [a3], [a5] [a6], [a15]).
The scattering data are in one-to-one correspondence with the spectral function [a6] [a7], [a13]. Recovery of $q ( x )$ given the spectral function is discussed in [a1], [a3], [a5], [a6].
The original work of M.G. Krein [a2] and its review in [a1] do not contain proofs. A detailed presentation of Krein's theory with complete proofs is given in [a15] for the first time. Also, a proof of consistency of Krein's method is given in [a15]. In [a2] (and in [a1]) there is no discussion of the consistency of Krein's method. By the consistency of an inversion method one means a proof of the implication $q \Rightarrow \mathcal{S}$ (the reconstructed potential generates the data from which it was reconstructed).
Below, Krein's method is described under the simplifying assumption $\kappa = 0$ (no bound states and no resonance at $k = 0$). The general case is treated in [a15].'
|
In Step 1, one can find $f ( k )$ by a different method: Solve the Riemann problem
\begin{equation} \tag{a5} \varphi_{+} ( k ) = S ( - k ) \varphi _ { - } ( k ), \end{equation}
\begin{equation*} k \in \mathbf{R} , \varphi _ { \pm } ( \infty ) = 1. \end{equation*}
If $\operatorname{ind} S ( k ) = 0$, this problem has the unique solution $\{ \varphi_+ ( k ) , \varphi_- ( k ) \}$. One has $\varphi _ { + } ( k ) = f ( k )$, $\varphi_{-} ( k ) = f ( - k )$.
Note that the data $\mathcal{S}$ allow one to find a unique $f ( k )$ by solving the Riemann problem (a5) with the additional conditions: $\varphi_{+} ( k )$ has $J$ simple zeros at the points $i k_j$ if $\kappa = - 2 J$ and, if $\kappa = - 2 J - 1$, $\varphi_{+} ( k )$ has, in addition, a simple zero at $k = 0$. Thus, the data $\mathcal{S}$ is equivalent to the data $\{ f ( k ) , s _j 1 \leq j \leq J \}$.
An inverse problem of recovery of $q ( x )$ from incomplete scattering data but with an a priori assumption that $q ( x )$ has compact support is investigated in [a8] [a9]. It is proved that if $q \in L _ { 1 , 1} $ is compactly supported and if $\delta ( k )$ is known for a sequence $k = k _ { n } > 0$ which has a finite limit point inside $( 0 , \infty )$, then $q ( x )$ is determined uniquely. An algorithm for finding a compactly supported $q ( x )$ from $\delta ( k )$ (that is, from $\mathcal{S} ( k )$) known for all $k > 0$ is given in [a8]. A uniqueness theorem for the problem of finding a compactly supported $q ( x )$ from the knowledge of $f ^ { \prime } ( 0 , k )$, $\forall k > 0$, is proved in [a13].
In [a7], [a12] an algorithm for recovery of $q ( x )$ from the $I$-function is given, where the $I$-function is identical with the Weyl function.
For $q \in L _ { 1 , 1} $ to belong to $L ^ { 2 } ( \mathbf{R} _ { + } )$ it is necessary and sufficient [a6] that
\begin{equation} \tag{a6} k \left[ 1 - S ( k ) + \frac { Q } { i k } \right] \in L ^ { 2 } ( \mathbf{R} ), \end{equation}
where
\begin{equation*} Q : = \int _ { 0 } ^ { \infty } q ( t ) d t = - 2 i \operatorname { lim } _ { k \rightarrow \infty } \{ k [ f ( k ) - 1 ] \}. \end{equation*}
If $q ( x ) \in L _ { 1,1 } \cap L ^ { 2 } ( \mathbf{R} _ { + } )$, $q = 0$ for $x \geq a$, is compactly supported, then $f ( k )$ is an entire function of exponential type $\leq 2 a$. Its zeros in $\mathbf{C} _ { - } : = \{ k : \operatorname { Im } k < 0 \}$ are called resonances.
If $q ( x ) \not\equiv 0$, $\int _ { 0 } ^ { \infty } x ^ { n } | q ( x ) | d x = o ( n ^ { b n } )$, $0 \leq b < 1$, then there are infinitely many resonances [a6].
There exists a $q ( x ) \in C _ { 0 } ^ { \infty } ( \mathbf{R} + )$, $q ( x ) = 0$ for $x \geq \epsilon$, where $\epsilon > 0$ is arbitrary small, which generates infinitely many purely imaginary resonances [a6].
If $q ( x ) \in L _ { 1,1 }$, $q ( x ) = 0$ for $x \geq a$ and $q ( x )$ does not change sign in an interval $( a - \delta , a )$, where $\delta > 0$ is arbitrarily small, then $q ( x )$ generates only finitely many purely imaginary resonances (a6).
If $q \in L _ { 1 , 1} $, then the following estimate (see [a5]) is useful:
\begin{equation*} \left| F ^ { \prime } ( 2 x ) - \frac { q ( x ) } { 4 } + \frac { 1 } { 4 } \left( \int _ { x } ^ { \infty } q ( t ) d t \right)^2 \right| \leq c \sigma ^ { 2 } ( x ), \end{equation*}
\begin{equation*} \sigma ( x ) : = \int _ { x } ^ { \infty } | q ( t ) | d t. \end{equation*}
The Jost solution $f ( x , k )$ can be written as $f ( x , k ) = e ^ { i k x } + \int _ { x } ^ { \infty } A ( x , y ) e ^ { i k y } d y$, where $A ( x , y )$ is the kernel of the transformation operator. If $q \in L _ { 1 , 1} $, then
\begin{equation*} | F ( 2 x ) + A ( x , x ) | \leq c \sigma ( x ), \end{equation*}
\begin{equation*} | F ( 2 x ) | \leq c \sigma ( x ) , | A ( x , y ) | \leq c \sigma \left( \frac { x + y } { 2 } \right) , \end{equation*}
\begin{equation*} \left| \frac { \partial A ( x , y ) } { \partial x } + \frac { 1 } { 4 } q \left( \frac { x + y } { 2 } \right) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right) , \left| \frac { \partial A ( x , y ) } { \partial y } + \frac { 1 } { 4 } q ( \frac { x + y } { 2 } ) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right), \end{equation*}
where $c > 0$ is a constant. The function $A ( x , y )$ solves the Volterra-type equation
\begin{equation*} A ( x , y ) = \frac { 1 } { 2 } \int _ { ( x + y ) / 2 } ^ { \infty } q ( t ) d t + \end{equation*}
\begin{equation*} + \int _ { \frac { x + y } { 2 } } ^ { \infty } d s \int _ { 0 } ^ { \frac { y - x } { 2 } } q ( s - t ) A ( s - t , s + t ) d t. \end{equation*}
If $q \in L _ { 1 , 1} $ and $q ( x ) = 0$ for $x > a$, then $A ( x , y ) = 0$ for $y \geq x \geq a$, $F ( x ) = 0$ for $x = 2 a$, and $A ( y ) : = A ( 0 , y ) = 0$ for $y \geq 2 a$. Since $f ( k ) = 1 + \int _ { 0 } ^ { \infty } A ( y ) e ^ { i k y } d y$, it follows that $f ( k )$ is an entire function of order $1$ and type $\leq 2 a$, and $S ( k ) = f ( - k ) / f ( k )$ is meromorphic on the whole complex $k$-plane (cf. also Meromorphic function).
Conversely, if the scattering data $\mathcal{S}$ correspond to a $q \in L _ { 1 , 1} $ (necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function $f ( k )$ which is an entire function of exponential type $\leq 2 a$, then $q ( x ) = 0$ for $x > a$, (see [a6]).
References
| [a1] | K. Chadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989) |
| [a2] | M. Krein, "Theory of accelerants and $S$-matrices of canonical differential systems" Dokl. Akad. Nauk. USSR , III : 6 (1956) pp. 1167–1170 (In Russian) |
| [a3] | B. Levitan, "Inverse Sturm–Liouville problems" , VNU Press (1987) |
| [a4] | V. Marchenko, "Stability in the inverse problem of scattering theory" Mat. Sb. , 77 (1968) pp. 139–162 (In Russian) |
| [a5] | V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) |
| [a6] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a7] | A.G. Ramm, "Recovery of the potential from I-function" Math. Rept. Acad. Sci. Canada , 9 (1987) pp. 177–182 |
| [a8] | A.G. Ramm, "Recovery of compactly supported spherically symmetric potentials from the phase shift of $s$-wave" A.G. Ramm (ed.) , Spectral and Scattering Theory , Plenum (1998) pp. 111–130 |
| [a9] | A.G. Ramm, "Compactly supported spherically symmetric potentials are uniquely determined by the phase shift of $s$-wave" Phys. Lett. A , 242 : 4–5 (1998) pp. 215–219 |
| [a10] | A.G. Ramm, "Recovery of a quarkonium system from experimental data" J. Phys. A , 31 : 15 (1998) pp. L295–L299 |
| [a11] | A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" Comm. Math. Phys. , 207 : 1 (1999) pp. 231–247 |
| [a12] | A.G. Ramm, "Property C for ODE and applications to inverse scattering" Z. Angew. Anal. , 18 : 2 (1999) pp. 331–348 |
| [a13] | A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory and Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 15–75 |
| [a14] | A.G. Ramm, W. Scheid, "An approximate method for solving inverse scattering problem with fixed-energy data" J. Inverse Ill-Posed Probl. , 7 : 6 (1999) pp. 561–571 |
| [a15] | A.G. Ramm, "Krein's method in inverse scattering" , Operator Theory and Applications , Amer. Math. Soc. (2000) pp. 441–456 |
Inverse scattering, half-axis case. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_scattering,_half-axis_case&oldid=50412