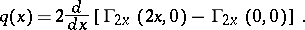Inverse scattering, half-axis case
The direct scattering problem on the half-axis consists of finding the solution 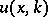 to the problem
to the problem
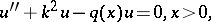 | (a1) |
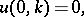 | (a2) |
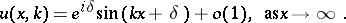 | (a3) |
Here, 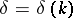 is to be determined. The function
is to be determined. The function 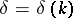 is called the phase shift. The coefficient
is called the phase shift. The coefficient 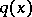 is called the scattering potential. It is assumed to be a real-valued function in the class
is called the scattering potential. It is assumed to be a real-valued function in the class
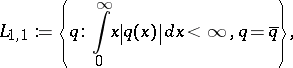 |
where the bar stands for complex conjugation. The solution 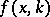 to (a1) which satisfies the relation
to (a1) which satisfies the relation 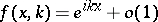 , as
, as 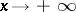 , is called the Jost solution. The function
, is called the Jost solution. The function 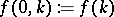 is called the Jost function. One has
is called the Jost function. One has
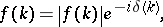 |
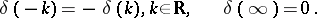 |
If 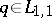 , then
, then 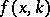 exists and is unique,
exists and is unique, 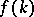 is analytic in
is analytic in 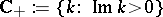 and has at most finitely many zeros in
and has at most finitely many zeros in 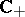 , all of which are simple and of the form
, all of which are simple and of the form 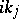 ,
, 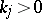 ,
, 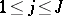 . The numbers
. The numbers 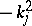 are the eigenvalues of the self-adjoint operator
are the eigenvalues of the self-adjoint operator
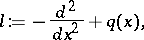 |
which is determined by the Dirichlet boundary condition at 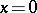 in the Hilbert space
in the Hilbert space 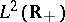 ,
, 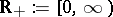 (cf. also Dirichlet boundary conditions). In physics,
(cf. also Dirichlet boundary conditions). In physics, 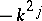 are called the bound states. The positive numbers
are called the bound states. The positive numbers 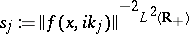 are called the norming constants. The function
are called the norming constants. The function  is called the
is called the 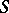 -matrix (cf. Scattering matrix). The triple
-matrix (cf. Scattering matrix). The triple 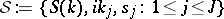 is called the scattering data.
is called the scattering data.
The inverse scattering problem consists of finding 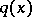 given
given 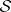 .
.
The point 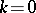 can also be a zero of
can also be a zero of 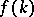 . It is called a resonance at
. It is called a resonance at 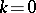 . If
. If 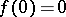 , then
, then 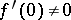 . The basic results of inverse scattering theory are (see [a5], [a6]):
. The basic results of inverse scattering theory are (see [a5], [a6]):
1) The uniqueness theorem: 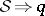 ; that is, the scattering data determine
; that is, the scattering data determine 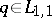 uniquely.
uniquely.
2) The reconstruction theorem: If 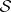 , corresponding to a
, corresponding to a 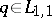 , is given, then
, is given, then 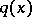 can be reconstructed by the Marchenko method, as follows:'
can be reconstructed by the Marchenko method, as follows:'
<tbody> </tbody>
|
3) The characterization theorem: For 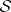 to be the scattering data corresponding to a
to be the scattering data corresponding to a 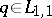 it is necessary and sufficient that the following conditions hold:
it is necessary and sufficient that the following conditions hold:
i) 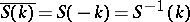 ,
, 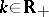 ;
; 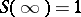 ,
, 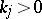 ,
, 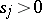 ,
, 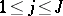 ;
;
ii) 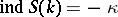 ,
,  or
or 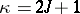 ;
;
iii) 
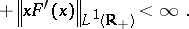 |
Here, 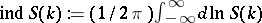 .
.
Note that 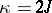 if
if 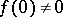 , and
, and 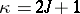 if
if 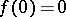 . The mapping
. The mapping 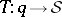 is a homeomorphism between
is a homeomorphism between 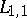 and the space of the scattering data equipped with the norm
and the space of the scattering data equipped with the norm 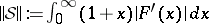 (see [a4], [a5] [a6]).
(see [a4], [a5] [a6]).
One can prove (see [a6], [a13]) the diagram
 |
each step of which is invertible. Here, 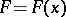 and
and 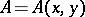 are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that
are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that 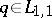 or
or 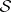 satisfies the characterization conditions).
satisfies the characterization conditions).
Other methods for solving the inverse scattering problem on the half-axis are based on the solution of the inverse problem of recovery of 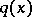 from the spectral function
from the spectral function  (
( ) and the Krein method ([a1], [a3], [a5] [a6], [a15]).
) and the Krein method ([a1], [a3], [a5] [a6], [a15]).
The scattering data are in one-to-one correspondence with the spectral function [a6] [a7], [a13]. Recovery of 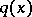 given the spectral function is discussed in [a1], [a3], [a5], [a6].
given the spectral function is discussed in [a1], [a3], [a5], [a6].
The original work of M.G. Krein [a2] and its review in [a1] do not contain proofs. A detailed presentation of Krein's theory with complete proofs is given in [a15] for the first time. Also, a proof of consistency of Krein's method is given in [a15]. In [a2] (and in [a1]) there is no discussion of the consistency of Krein's method. By the consistency of an inversion method one means a proof of the implication 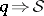 (the reconstructed potential generates the data from which it was reconstructed).
(the reconstructed potential generates the data from which it was reconstructed).
Below, Krein's method is described under the simplifying assumption 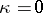 (no bound states and no resonance at
(no bound states and no resonance at 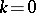 ). The general case is treated in [a15].'
). The general case is treated in [a15].'
<tbody> </tbody>
|
In Step 1, one can find 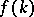 by a different method: Solve the Riemann problem
by a different method: Solve the Riemann problem
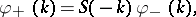 | (a5) |
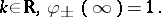 |
If  , this problem has the unique solution
, this problem has the unique solution 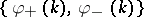 . One has
. One has 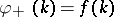 ,
, 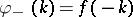 .
.
Note that the data 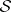 allow one to find a unique
allow one to find a unique 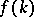 by solving the Riemann problem (a5) with the additional conditions:
by solving the Riemann problem (a5) with the additional conditions: 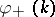 has
has 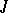 simple zeros at the points
simple zeros at the points 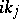 if
if 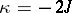 and, if
and, if 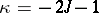 ,
, 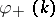 has, in addition, a simple zero at
has, in addition, a simple zero at 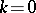 . Thus, the data
. Thus, the data 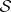 is equivalent to the data
is equivalent to the data 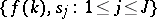 .
.
An inverse problem of recovery of 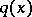 from incomplete scattering data but with an a priori assumption that
from incomplete scattering data but with an a priori assumption that 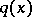 has compact support is investigated in [a8] [a9]. It is proved that if
has compact support is investigated in [a8] [a9]. It is proved that if 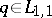 is compactly supported and if
is compactly supported and if 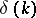 is known for a sequence
is known for a sequence 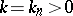 which has a finite limit point inside
which has a finite limit point inside 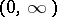 , then
, then 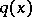 is determined uniquely. An algorithm for finding a compactly supported
is determined uniquely. An algorithm for finding a compactly supported 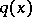 from
from 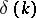 (that is, from
(that is, from 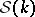 ) known for all
) known for all 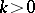 is given in [a8]. A uniqueness theorem for the problem of finding a compactly supported
is given in [a8]. A uniqueness theorem for the problem of finding a compactly supported 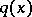 from the knowledge of
from the knowledge of 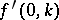 ,
, 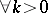 , is proved in [a13].
, is proved in [a13].
In [a7], [a12] an algorithm for recovery of 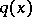 from the
from the 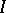 -function is given, where the
-function is given, where the 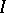 -function is identical with the Weyl function.
-function is identical with the Weyl function.
For 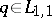 to belong to
to belong to 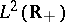 it is necessary and sufficient [a6] that
it is necessary and sufficient [a6] that
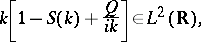 | (a6) |
where
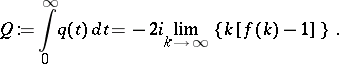 |
If 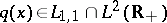 ,
, 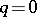 for
for 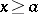 , is compactly supported, then
, is compactly supported, then 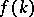 is an entire function of exponential type
is an entire function of exponential type 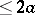 . Its zeros in
. Its zeros in 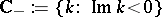 are called resonances.
are called resonances.
If 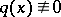 ,
, 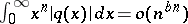 ,
, 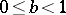 , then there are infinitely many resonances [a6].
, then there are infinitely many resonances [a6].
There exists a 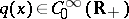 ,
, 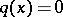 for
for 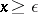 , where
, where 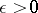 is arbitrary small, which generates infinitely many purely imaginary resonances [a6].
is arbitrary small, which generates infinitely many purely imaginary resonances [a6].
If 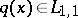 ,
, 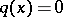 for
for 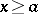 and
and 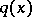 does not change sign in an interval
does not change sign in an interval  , where
, where 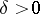 is arbitrarily small, then
is arbitrarily small, then 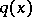 generates only finitely many purely imaginary resonances (a6).
generates only finitely many purely imaginary resonances (a6).
If 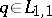 , then the following estimate (see [a5]) is useful:
, then the following estimate (see [a5]) is useful:
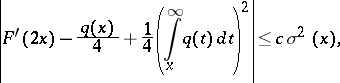 |
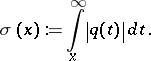 |
The Jost solution 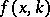 can be written as
can be written as 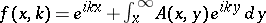 , where
, where 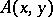 is the kernel of the transformation operator. If
is the kernel of the transformation operator. If 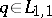 , then
, then
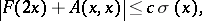 |
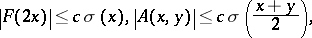 |
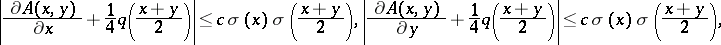 |
where 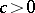 is a constant. The function
is a constant. The function 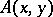 solves the Volterra-type equation
solves the Volterra-type equation
 |
 |
If 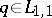 and
and 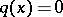 for
for 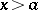 , then
, then 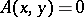 for
for 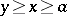 ,
, 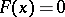 for
for  , and
, and 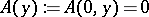 for
for 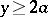 . Since
. Since 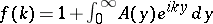 , it follows that
, it follows that 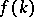 is an entire function of order
is an entire function of order 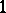 and type
and type 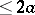 , and
, and  is meromorphic on the whole complex
is meromorphic on the whole complex 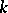 -plane (cf. also Meromorphic function).
-plane (cf. also Meromorphic function).
Conversely, if the scattering data 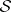 correspond to a
correspond to a 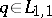 (necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function
(necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function 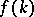 which is an entire function of exponential type
which is an entire function of exponential type 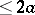 , then
, then 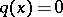 for
for 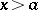 , (see [a6]).
, (see [a6]).
References
| [a1] | K. Chadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989) |
| [a2] | M. Krein, "Theory of accelerants and 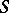 -matrices of canonical differential systems" Dokl. Akad. Nauk. USSR , III : 6 (1956) pp. 1167–1170 (In Russian) -matrices of canonical differential systems" Dokl. Akad. Nauk. USSR , III : 6 (1956) pp. 1167–1170 (In Russian) |
| [a3] | B. Levitan, "Inverse Sturm–Liouville problems" , VNU Press (1987) |
| [a4] | V. Marchenko, "Stability in the inverse problem of scattering theory" Mat. Sb. , 77 (1968) pp. 139–162 (In Russian) |
| [a5] | V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) |
| [a6] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a7] | A.G. Ramm, "Recovery of the potential from I-function" Math. Rept. Acad. Sci. Canada , 9 (1987) pp. 177–182 |
| [a8] | A.G. Ramm, "Recovery of compactly supported spherically symmetric potentials from the phase shift of  -wave" A.G. Ramm (ed.) , Spectral and Scattering Theory , Plenum (1998) pp. 111–130 -wave" A.G. Ramm (ed.) , Spectral and Scattering Theory , Plenum (1998) pp. 111–130 |
| [a9] | A.G. Ramm, "Compactly supported spherically symmetric potentials are uniquely determined by the phase shift of  -wave" Phys. Lett. A , 242 : 4–5 (1998) pp. 215–219 -wave" Phys. Lett. A , 242 : 4–5 (1998) pp. 215–219 |
| [a10] | A.G. Ramm, "Recovery of a quarkonium system from experimental data" J. Phys. A , 31 : 15 (1998) pp. L295–L299 |
| [a11] | A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" Comm. Math. Phys. , 207 : 1 (1999) pp. 231–247 |
| [a12] | A.G. Ramm, "Property C for ODE and applications to inverse scattering" Z. Angew. Anal. , 18 : 2 (1999) pp. 331–348 |
| [a13] | A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory and Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 15–75 |
| [a14] | A.G. Ramm, W. Scheid, "An approximate method for solving inverse scattering problem with fixed-energy data" J. Inverse Ill-Posed Probl. , 7 : 6 (1999) pp. 561–571 |
| [a15] | A.G. Ramm, "Krein's method in inverse scattering" , Operator Theory and Applications , Amer. Math. Soc. (2000) pp. 441–456 |
Inverse scattering, half-axis case. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_scattering,_half-axis_case&oldid=16304
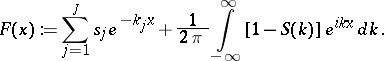
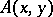 :
:
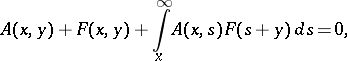
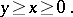
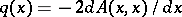 .
.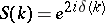 ,
, 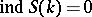 ,
, 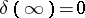 , one finds
, one finds 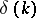 , then calculates
, then calculates
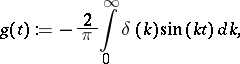
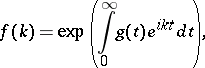
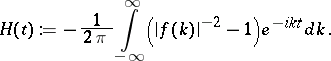
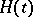 , one solves the equation
, one solves the equation
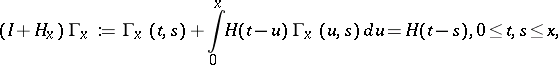
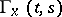 and finds
and finds 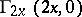 ,
, 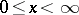 .
.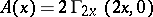 , and calculates
, and calculates 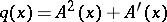 . Alternatively,
. Alternatively,