Difference between revisions of "Markov braid theorem"
From Encyclopedia of Mathematics
m (AUTOMATIC EDIT (latexlist): Replaced 7 formulas out of 9 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 9 formulas, 7 were replaced by TEX code.--> | Out of 9 formulas, 7 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
If two closed braids represent the same ambient isotopy class of oriented links (cf. also [[Braid theory|Braid theory]]), then one can transform one braid to another by a sequence of Markov moves: | If two closed braids represent the same ambient isotopy class of oriented links (cf. also [[Braid theory|Braid theory]]), then one can transform one braid to another by a sequence of Markov moves: | ||
Revision as of 17:44, 1 July 2020
If two closed braids represent the same ambient isotopy class of oriented links (cf. also Braid theory), then one can transform one braid to another by a sequence of Markov moves:
i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation).
ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th braid group
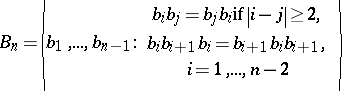 |
and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group.
Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the Jones–Conway polynomial).
References
| [a1] | J.S. Birman, "Braids, links and mapping class groups" , Ann. of Math. Stud. , 82 , Princeton Univ. Press (1974) |
| [a2] | A.A. Markov, "Über die freie Aquivalenz der geschlossen Zopfe" Recueil Math. Moscou , 1 (1935) pp. 73–78 |
| [a3] | N.M. Weinberg, "On free equivalence of free braids" C.R. (Dokl.) Acad. Sci. USSR , 23 (1939) pp. 215–216 (In Russian) |
How to Cite This Entry:
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=50123
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=50123
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article