Difference between revisions of "Addition theorems in the theory of special functions"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (spaces) |
||
| Line 32: | Line 32: | ||
$ \Lambda $ | $ \Lambda $ | ||
a fixed elementary function, cf. also [[Elementary functions|Elementary functions]]) explicitly and orthogonally in terms of certain special functions $ \psi _ \mu ( t ) $ | a fixed elementary function, cf. also [[Elementary functions|Elementary functions]]) explicitly and orthogonally in terms of certain special functions $ \psi _ \mu ( t ) $ | ||
| − | with expansion coefficients of the form $ \textrm{ const } \ | + | with expansion coefficients of the form $ \textrm{ const } \ \phi _ \lambda ^ \mu ( x ) \ \phi _ \lambda ^ \mu ( y ) $. |
The $ \phi _ \lambda ^ \mu $ | The $ \phi _ \lambda ^ \mu $ | ||
are special functions associated with $ \phi _ \lambda $. | are special functions associated with $ \phi _ \lambda $. | ||
Revision as of 20:54, 4 April 2020
The exponential function satisfies the addition formula $ e ^ {x + y } = e ^ {x} e ^ {y} $.
More generally, the function $ f $
satisfies an algebraic addition theorem if $ A ( f ( x ) ,f ( y ) ,f ( x + y ) ) $
is identically zero for some polynomial $ A ( x,y,z ) $.
By a theorem of K. Weierstrass, a single-valued analytic function $ f ( z ) $
satisfying an algebraic addition theorem is either a rational function in $ z $,
or a rational function in $ e ^ {\lambda z } $
for some $ \lambda $,
or an elliptic function.
The addition formula for Legendre polynomials $ P _ {n} ( x ) $( P.S. Laplace, 1872) is the prototype of an addition theorem of a more general nature. It gives the explicit Fourier-cosine expansion of $ P _ {n} ( \cos \phi \cos \psi + \sin \phi \sin \psi \cos \theta ) $ in terms of $ \cos m \theta $. The Fourier coefficients depending on $ \phi $ and $ \psi $ factorize as products of two associated Legendre functions. This addition formula was generalized by L. Gegenbauer (1875) to ultraspherical polynomials and, more generally, by T.H. Koornwinder (1972) to Jacobi polynomials. Addition theorems of this type exist for a large number of special functions of hypergeometric type. See, in particular, [a6] for several addition formulas for Bessel functions.
An addition formula for a family of special functions $ \phi _ \lambda $ expands $ \phi _ \lambda ( \Lambda ( x,y,t ) ) $( $ \Lambda $ a fixed elementary function, cf. also Elementary functions) explicitly and orthogonally in terms of certain special functions $ \psi _ \mu ( t ) $ with expansion coefficients of the form $ \textrm{ const } \ \phi _ \lambda ^ \mu ( x ) \ \phi _ \lambda ^ \mu ( y ) $. The $ \phi _ \lambda ^ \mu $ are special functions associated with $ \phi _ \lambda $. A further requirement is that $ \psi _ {0} ( t ) = 1 $ and $ \phi _ \lambda ^ {0} = \phi _ \lambda $. A variant, in particular occurring for $ q $- special functions, is that $ \phi _ \lambda ( t ) $, or even $ \phi _ \lambda ( t ) \psi ^ {( x,y ) } _ \nu ( t ) $, is expanded in terms of $ \psi _ \mu ^ {( x,y ) } ( t ) $, with expansion coefficients as before. An important corollary of any addition formula is the product formula giving $ \phi _ \lambda ( x ) \phi _ \lambda ( y ) $ as an integral of $ \phi _ \lambda $.
Usually, if an addition formula is already explicitly given, then an analytic proof can be provided, but it is difficult to conjecture the form of an addition formula from scratch. Addition formulas can often be conceptually obtained by an interpretation on groups (Lie groups [a4], [a5]; finite groups [a3]; quantum groups [a2]) from the homomorphism property of a group representation and specific knowledge of the matrix coefficients of these representations in terms of special functions (cf. Special functions). Addition formulas with more general parameter values then follow by analytic continuation and by certain elementary operations.
Addition formulas are important because they encode in a relatively compact form a lot of information, for instance other identities, inequalities, positivity results (hypergroup structures, cf. Generalized displacement operators) for convolution and dual convolution associated with the $ \phi _ \lambda $, and sometimes unitariness of related group representations.
References
| [a1] | R. Askey, "Orthogonal polynomials and special functions" , Reg. Conf. Ser. Appl. Math. , 21 , SIAM (1975) |
| [a2] | E. Koelink, "Addition formulas for 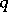 -special functions" M.E.H. Ismail et al. (ed.) , Special Functions, -special functions" M.E.H. Ismail et al. (ed.) , Special Functions,  -Series and Related Topics , Fields Inst. Commun. , 14 , Amer. Math. Soc. (1997) pp. 109–129 -Series and Related Topics , Fields Inst. Commun. , 14 , Amer. Math. Soc. (1997) pp. 109–129 |
| [a3] | D. Stanton, "Orthogonal polynomials and Chevalley groups" R.A. Askey (ed.) etAAsal. (ed.) , Special Functions: Group Theoretical Aspects and Applications (1984) pp. 87–128 |
| [a4] | N.J. Vilenkin, "Special functions and the theory of group representations" , Transl. Math. Monographs , 22 , Amer. Math. Soc. (1968) (In Russian) |
| [a5] | N.J. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , 1–3 , Kluwer Acad. Publ. (1991–1993) (In Russian) |
| [a6] | G.N. Watson, "Theory of Bessel functions" , Cambridge Univ. Press (1944) (Edition: Second) |
Addition theorems in the theory of special functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Addition_theorems_in_the_theory_of_special_functions&oldid=45026