Difference between revisions of "Quasi-symmetric function"
m (typo) |
|||
| Line 10: | Line 10: | ||
Products and sums of quasi-symmetric polynomials and power series are again quasi-symmetric (obviously), and thus one has, for example, the ring of quasi-symmetric power series | Products and sums of quasi-symmetric polynomials and power series are again quasi-symmetric (obviously), and thus one has, for example, the ring of quasi-symmetric power series | ||
| − | + | $$ | |
| − | + | \widehat{ \mathbf{Q}^{\mathrm{sym}}_{\mathbf{Z}}(X)) } | |
| − | + | $$ | |
in countably many commuting variables over the integers and its subring | in countably many commuting variables over the integers and its subring | ||
| − | + | $$ | |
| − | + | \mathbf{Q}^{\mathrm{sym}}_{\mathbf{Z}}(X)) | |
| − | + | $$ | |
of quasi-symmetric polynomials in finite of countably many indeterminates, which are the quasi-symmetric power series of bounded degree. | of quasi-symmetric polynomials in finite of countably many indeterminates, which are the quasi-symmetric power series of bounded degree. | ||
| Line 25: | Line 25: | ||
defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006025.png" />. These form a basis over the integers of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006026.png" />. | defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006025.png" />. These form a basis over the integers of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006026.png" />. | ||
| − | The algebra of quasi-symmetric functions is dual to the [[ | + | The algebra of quasi-symmetric functions is dual to the [[Leibniz–Hopf algebra]], or, equivalently to the Solomon descent algebra, more precisely, to the direct sum |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006027.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120060/q12006027.png" /></td> </tr></table> | ||
Revision as of 16:35, 28 March 2018
quasi-symmetric polynomial (in combinatorics)
Let $X$ be a finite or infinite set (of variables) and consider the ring of polynomials $R[X]$ and the ring of power series $R[[X]]$ over a commutative ring $R$ with unit element in the commuting variables from $X$. A polynomial or power series $f(X) \in R[[X]]$ is called symmetric if for any two finite sequences of indeterminates $X_1,\ldots,X_n$ and $Y_1,\ldots,Y_n$ from $X$ and any sequence of exponents $i_1,\ldots,i_n \in \mathbf{N}$, the coefficients in $f$ of $X_1^{i_1} \cdots X_n^{i_n}$ and $Y_1^{i_1} \cdots Y_n^{i_n}$ are the same.
Quasi-symmetric formal power series are a generalization introduced by I.M. Gessel, [a2], in connection with the combinatorics of plane partitions and descent sets of permutations [a3]. This time one takes a totally ordered set of indeterminates, e.g. $V = \{V_1,V_2,\ldots\}$, with the ordering that of the natural numbers, and the condition is that the coefficients of $X_1^{i_1} \cdots X_n^{i_n}$ and $Y_1^{i_1} \cdots Y_n^{i_n}$ are equal for all totally ordered sets of indeterminates $X_1 < \ldots < X_n$ and $Y_1 < \ldots < Y_n$. For example, $$ X_1 X_2^2 + X_1 X_3^2 + X_2 X_3^2 $$ is a quasi-symmetric polynomial in three variables that is not symmetric.
Products and sums of quasi-symmetric polynomials and power series are again quasi-symmetric (obviously), and thus one has, for example, the ring of quasi-symmetric power series $$ \widehat{ \mathbf{Q}^{\mathrm{sym}}_{\mathbf{Z}}(X)) } $$ in countably many commuting variables over the integers and its subring $$ \mathbf{Q}^{\mathrm{sym}}_{\mathbf{Z}}(X)) $$ of quasi-symmetric polynomials in finite of countably many indeterminates, which are the quasi-symmetric power series of bounded degree.
Given a word 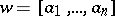 over
over 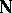 , also called a composition in this context, consider the quasi-monomial function
, also called a composition in this context, consider the quasi-monomial function
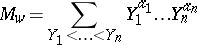 |
defined by 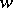 . These form a basis over the integers of
. These form a basis over the integers of 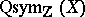 .
.
The algebra of quasi-symmetric functions is dual to the Leibniz–Hopf algebra, or, equivalently to the Solomon descent algebra, more precisely, to the direct sum
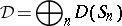 |
of the Solomon descent algebras 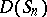 of the symmetric groups (cf. also Symmetric group), [a5], with a new multiplication over which the direct sum of the original multiplications is distributive. See [a1], [a4].
of the symmetric groups (cf. also Symmetric group), [a5], with a new multiplication over which the direct sum of the original multiplications is distributive. See [a1], [a4].
The algebra of quasi-symmetric functions in countably many indeterminates over the integers, 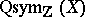 , is a free polynomial algebra over the integers, [a6].
, is a free polynomial algebra over the integers, [a6].
There is a completely different notion in the theory of functions of a complex variable that also goes by the name quasi-symmetric function; cf., e.g., [a7].
References
| [a1] | I.M. Gel'fand, D. Krob, A. Lascoux, B. Leclerc, V.S. Retakh, J.-Y. Thibon, "Noncommutative symmetric functions" Adv. Math. , 112 (1995) pp. 218–348 |
| [a2] | I.M. Gessel, "Multipartite 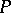 -partitions and inner product of skew Schur functions" Contemp. Math. , 34 (1984) pp. 289–301 -partitions and inner product of skew Schur functions" Contemp. Math. , 34 (1984) pp. 289–301 |
| [a3] | I.M. Gessel, Ch. Reutenauer, "Counting permutations with given cycle-structure and descent set" J. Combin. Th. A , 64 (1993) pp. 189–215 |
| [a4] | C. Malvenuto, Ch. Reutenauer, "Duality between quasi-symmetric functions and the Solomon descent algebra" J. Algebra , 177 (1994) pp. 967–982 |
| [a5] | L. Solomon, "A Mackey formula in the group ring of a Coxeter group" J. Algebra , 41 (1976) pp. 255–268 |
| [a6] | M. Hazewinkel, "The algebra of quasi-symmetric functions is free over the integers" Preprint CWI (Amsterdam) and ICTP (Trieste) (1999) |
| [a7] | M. Chuaqui, B. Osgood, "Weak Schwarzians, bounded hyperbolic distortion, and smooth quasi-symmetric functions" J. d'Anal. Math. , 68 (1996) pp. 209–252 |
Quasi-symmetric function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-symmetric_function&oldid=43035