Difference between revisions of "Derangement"
(links) |
m (typo) |
||
| Line 1: | Line 1: | ||
''derangement'' | ''derangement'' | ||
| − | A permutation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524301.png" /> elements in which the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524302.png" /> cannot occupy the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524303.png" />-th position, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524304.png" />. The problem of calculating the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524305.png" /> of derangements is known as the "[[Montmort matching problem]]" or "problème des rencontres" (cf. [[Classical combinatorial problems]]. The following formula holds: | + | A permutation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524301.png" /> elements in which the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524302.png" /> cannot occupy the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524303.png" />-th position, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524304.png" />. The problem of calculating the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524305.png" /> of derangements is known as the "[[Montmort matching problem]]" or "problème des rencontres" (cf. [[Classical combinatorial problems]]). The following formula holds: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524306.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052430/i0524306.png" /></td> </tr></table> | ||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H.J. Ryser, "Combinatorial mathematics" , ''Carus Math. Monogr.'' , '''14''' , Wiley & Math. Assoc. Amer. (1963)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Riordan, "An introduction to combinatorial mathematics" , Wiley (1958)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> H.J. Ryser, "Combinatorial mathematics" , ''Carus Math. Monogr.'' , '''14''' , Wiley & Math. Assoc. Amer. (1963)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> J. Riordan, "An introduction to combinatorial mathematics" , Wiley (1958)</TD></TR> | ||
| + | </table> | ||
Revision as of 07:28, 2 December 2016
derangement
A permutation of  elements in which the element
elements in which the element 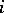 cannot occupy the
cannot occupy the 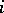 -th position,
-th position, 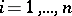 . The problem of calculating the number
. The problem of calculating the number 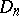 of derangements is known as the "Montmort matching problem" or "problème des rencontres" (cf. Classical combinatorial problems). The following formula holds:
of derangements is known as the "Montmort matching problem" or "problème des rencontres" (cf. Classical combinatorial problems). The following formula holds:
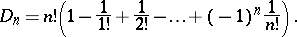 |
Derangements are a special case of permutations satisfying a specific restriction on the position of the permuted elements. For example, the "problème des ménages" consists in calculating the number 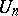 of permutations conflicting with the two permutations
of permutations conflicting with the two permutations 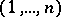 and
and 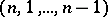 . (Two permutations of
. (Two permutations of  elements are called conflicting if the
elements are called conflicting if the 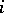 -th element occupies different positions in each of them for all
-th element occupies different positions in each of them for all  ). The number
). The number 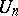 is given by the formula:
is given by the formula:
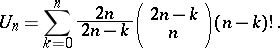 |
The number 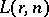 of Latin squares (cf. Latin square) of size
of Latin squares (cf. Latin square) of size 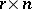 for
for  can be calculated in terms of
can be calculated in terms of 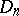 and
and  by the formulas
by the formulas
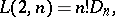 |
 |
References
| [1] | H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Wiley & Math. Assoc. Amer. (1963) |
| [2] | J. Riordan, "An introduction to combinatorial mathematics" , Wiley (1958) |
Derangement. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derangement&oldid=39881