Difference between revisions of "Primary ideal"
m (link) |
m (link) |
||
| Line 1: | Line 1: | ||
''of a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744601.png" />'' | ''of a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744601.png" />'' | ||
| − | An [[Ideal|ideal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744602.png" /> such that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744603.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744604.png" />, then either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744605.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744606.png" /> for some natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744607.png" />. In the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744608.png" /> of integers a primary ideal is an ideal of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744609.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446010.png" /> is a prime number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446011.png" /> is a natural number. In commutative algebra an important role is played by the representation of an arbitrary ideal of a commutative [[Noetherian ring|Noetherian ring]] as an intersection of a finite number of primary ideals — a [[Primary decomposition|primary decomposition]]. More generally, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446012.png" /> denote the set of prime ideals of a [[Ring|ring]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446013.png" /> that are annihilators of non-zero submodules of a [[Module|module]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446014.png" />. A submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446015.png" /> of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446016.png" /> over a Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446017.png" /> is called primary if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446018.png" /> is a one-element set. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446019.png" /> is commutative, then every proper submodule of a Noetherian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446020.png" />-module that cannot be represented as an intersection of submodules strictly containing it is primary. In the non-commutative case this is not true and therefore attempts have been undertaken to construct various non-commutative generalizations of the notion of primarity. E.g., a proper submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446021.png" /> of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446022.png" /> is called primary if for every non-zero injective submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446023.png" /> of the [[injective hull]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446024.png" /> of the module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446025.png" /> (cf. [[Injective module|Injective module]]) the intersection of the kernels of the homomorphisms from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446026.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446027.png" /> is trivial. Another successful generalization is the notion of a tertiary ideal [[#References|[4]]]: A left ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446028.png" /> of a left Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446029.png" /> is called tertiary if, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446031.png" />, it follows from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446032.png" /> that, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446033.png" />, there is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446034.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446035.png" />. Both these generalizations lead to a non-commutative analogue of primary decomposition. Every tertiary ideal of a Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446036.png" /> is primary if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446037.png" /> satisfies the Artin–Rees condition: For arbitrary left ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446038.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446039.png" /> there is a natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446040.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446041.png" /> (cf. [[#References|[3]]]). | + | An [[Ideal|ideal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744602.png" /> such that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744603.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744604.png" />, then either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744605.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744606.png" /> for some natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744607.png" />. In the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744608.png" /> of integers a primary ideal is an ideal of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p0744609.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446010.png" /> is a prime number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446011.png" /> is a natural number. In commutative algebra an important role is played by the representation of an arbitrary ideal of a commutative [[Noetherian ring|Noetherian ring]] as an intersection of a finite number of primary ideals — a [[Primary decomposition|primary decomposition]]. More generally, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446012.png" /> denote the set of prime ideals of a [[Ring|ring]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446013.png" /> that are annihilators of non-zero submodules of a [[Module|module]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446014.png" />. A submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446015.png" /> of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446016.png" /> over a Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446017.png" /> is called primary if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446018.png" /> is a one-element set. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446019.png" /> is commutative, then every proper submodule of a Noetherian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446020.png" />-module that cannot be represented as an intersection of submodules strictly containing it is primary. In the non-commutative case this is not true and therefore attempts have been undertaken to construct various non-commutative generalizations of the notion of primarity. E.g., a proper submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446021.png" /> of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446022.png" /> is called primary if for every non-zero injective submodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446023.png" /> of the [[injective hull]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446024.png" /> of the module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446025.png" /> (cf. [[Injective module|Injective module]]) the intersection of the kernels of the homomorphisms from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446026.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446027.png" /> is trivial. Another successful generalization is the notion of a [[tertiary ideal]] [[#References|[4]]]: A left ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446028.png" /> of a left Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446029.png" /> is called tertiary if, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446031.png" />, it follows from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446032.png" /> that, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446033.png" />, there is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446034.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446035.png" />. Both these generalizations lead to a non-commutative analogue of primary decomposition. Every tertiary ideal of a Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446036.png" /> is primary if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446037.png" /> satisfies the Artin–Rees condition: For arbitrary left ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446038.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446039.png" /> there is a natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446040.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074460/p07446041.png" /> (cf. [[#References|[3]]]). |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''1''' , Springer (1975)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> O. Goldman, "Rings and modules of quotients" ''J. of Algebra'' , '''13''' : 1 (1969) pp. 10–47</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Lesieur, R. Croisot, "Algèbre noethérienne noncommutative" , Gauthier-Villars (1963)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''1''' , Springer (1975)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> O. Goldman, "Rings and modules of quotients" ''J. of Algebra'' , '''13''' : 1 (1969) pp. 10–47</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Lesieur, R. Croisot, "Algèbre noethérienne noncommutative" , Gauthier-Villars (1963)</TD></TR></table> | ||
Revision as of 19:20, 5 October 2017
of a commutative ring 
An ideal  such that if
such that if  and
and  , then either
, then either  or
or  for some natural number
for some natural number  . In the ring
. In the ring  of integers a primary ideal is an ideal of the form
of integers a primary ideal is an ideal of the form  , where
, where 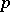 is a prime number and
is a prime number and  is a natural number. In commutative algebra an important role is played by the representation of an arbitrary ideal of a commutative Noetherian ring as an intersection of a finite number of primary ideals — a primary decomposition. More generally, let
is a natural number. In commutative algebra an important role is played by the representation of an arbitrary ideal of a commutative Noetherian ring as an intersection of a finite number of primary ideals — a primary decomposition. More generally, let 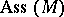 denote the set of prime ideals of a ring
denote the set of prime ideals of a ring  that are annihilators of non-zero submodules of a module
that are annihilators of non-zero submodules of a module 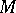 . A submodule
. A submodule  of a module
of a module  over a Noetherian ring
over a Noetherian ring  is called primary if
is called primary if  is a one-element set. If
is a one-element set. If  is commutative, then every proper submodule of a Noetherian
is commutative, then every proper submodule of a Noetherian  -module that cannot be represented as an intersection of submodules strictly containing it is primary. In the non-commutative case this is not true and therefore attempts have been undertaken to construct various non-commutative generalizations of the notion of primarity. E.g., a proper submodule
-module that cannot be represented as an intersection of submodules strictly containing it is primary. In the non-commutative case this is not true and therefore attempts have been undertaken to construct various non-commutative generalizations of the notion of primarity. E.g., a proper submodule 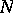 of a module
of a module  is called primary if for every non-zero injective submodule
is called primary if for every non-zero injective submodule  of the injective hull
of the injective hull  of the module
of the module 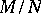 (cf. Injective module) the intersection of the kernels of the homomorphisms from
(cf. Injective module) the intersection of the kernels of the homomorphisms from 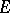 into
into 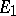 is trivial. Another successful generalization is the notion of a tertiary ideal [4]: A left ideal
is trivial. Another successful generalization is the notion of a tertiary ideal [4]: A left ideal  of a left Noetherian ring
of a left Noetherian ring  is called tertiary if, for any
is called tertiary if, for any 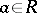 ,
, 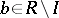 , it follows from
, it follows from  that, for any
that, for any  , there is an element
, there is an element 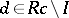 such that
such that  . Both these generalizations lead to a non-commutative analogue of primary decomposition. Every tertiary ideal of a Noetherian ring
. Both these generalizations lead to a non-commutative analogue of primary decomposition. Every tertiary ideal of a Noetherian ring 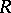 is primary if and only if
is primary if and only if  satisfies the Artin–Rees condition: For arbitrary left ideals
satisfies the Artin–Rees condition: For arbitrary left ideals  of
of  there is a natural number
there is a natural number  such that
such that 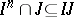 (cf. [3]).
(cf. [3]).
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [3] | O. Goldman, "Rings and modules of quotients" J. of Algebra , 13 : 1 (1969) pp. 10–47 |
| [4] | L. Lesieur, R. Croisot, "Algèbre noethérienne noncommutative" , Gauthier-Villars (1963) |
Primary ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primary_ideal&oldid=39565