Homological dimension

A numerical characteristic of an object in a category with respect to a certain specified class of objects in this category. The categories of modules over a ring form the principal range of application of this concept.

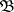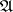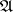Let be a fixed class of objects in an Abelian category , and let be an object in . The (projective) homological dimension of 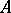with respect to 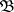is then defined as the least number for which there exists an exact sequence of the form

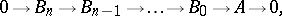where all 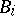are from 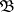. If such an does not exist, one says that the homological dimension of 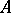is equal to .

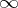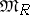Let (respectively, ) be the category of left (respectively, right) modules over an associative ring 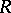with a unit element. Then: a) if is the class of all projective left 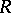-modules, then the corresponding homological dimension of 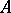is also called the projective dimension and is denoted by 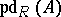; b) if 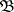is the class of all flat left 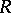-modules, then the corresponding homological dimension of 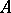is called the weak dimension and is denoted by 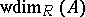. If 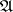is the category of left graded modules (cf. Graded module) over a graded ring 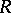and 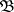is the class of all left projective graded 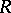-modules, then the corresponding homological dimension of a graded -module is called the graded projective dimension and is denoted by .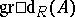

A dual construction may also be considered. If 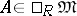, then the least number such that there exists an exact sequence

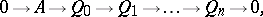where all the modules are injective, is said to be the injective dimension of 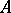and is denoted by .

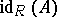For 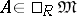the following conditions are equivalent:

a) ;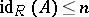

b) for all 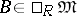(cf. Functor Ext);

b') 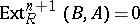for all cyclic modules ;

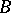c) 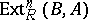is a right-exact functor of the argument ;

d) if

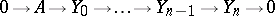is an exact sequence and if the modules 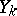are injective for 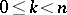, then 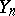is an injective module.

The following conditions are also equivalent:

a) ;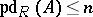

b) 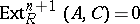for all ;

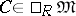c) 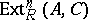is a right-exact functor of the argument ;

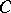d) if

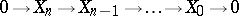is an exact sequence and if the modules 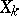are projective for 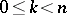, then 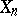is a projective module.

If the sequence

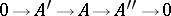is exact, where 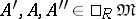, and if

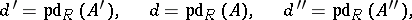then

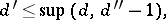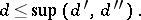If 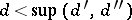, then .

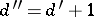The number

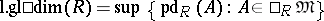is called the left global dimension of the ring .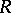

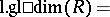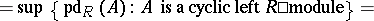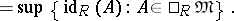If the ring 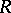has a composition series of left ideals, then

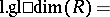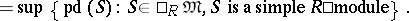The number

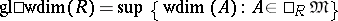is called the global weak dimension of the ring 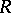, and

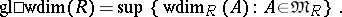The number

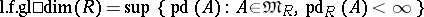is called the left bounded global dimension of the ring .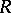

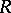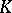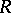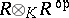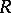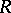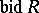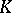The following dimensions are close to these. If is an algebra over a commutative ring , the projective dimension of the -bimodule of (i.e. 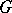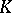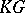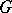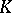of the left module , where is the opposite ring to ) is called the bidimension of the algebra and is denoted by ; if is a group, and is a commutative ring, then the (co) homological dimension of the group is by definition the flat (projective) dimension of the module over the group ring with the trivial action of on and is denoted by .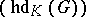

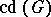A number of well-known theorems can be reformulated in terms of the homological dimension. Thus, the Wedderburn–Artin theorem has the following form: A ring 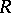is classically simple if and only if 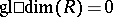. A ring 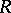is regular in the sense of von Neumann if and only if 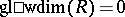. The equality 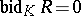for an algebra 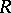over a field 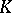is equivalent to its separability over 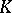. The statement that a subgroup of a free Abelian group is free is equivalent to saying that 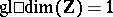, where 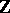is the ring of integers. A ring 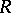for which 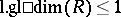is called a left hereditary ring.

The left and right global dimensions of a ring 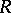need not coincide. If, on the other hand, is both left and right Noetherian, then

If is a ring homomorphism, then any 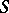-module 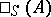can also be regarded as an 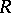-module, and

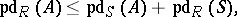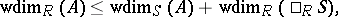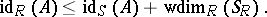If the ring is filtered, then

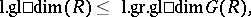where 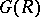is the associated graded ring.

In several cases the study of homological dimensions is related to the cardinality of the modules under consideration. This makes it possible, in particular, to estimate the difference between the weak and projective dimensions of a module, and also between the left and right global dimensions of the ring. The continuum hypothesis is equivalent to

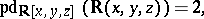where 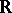is the field of real numbers, 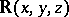is the field of rational functions and 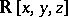is the ring of polynomials over .

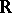The majority of studies on homological dimensions is concerned with discovering relations between these dimensions and other characteristics of modules and fields. Thus, according to the Hilbert syzygy theorem,

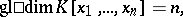where 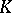is a field and 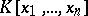is the ring of polynomials in the variables over . By now this theorem has been considerably generalized. The homological dimension of group algebras of solvable groups is closely connected with the length of the solvable series of the group and with the ranks of its factors. The equation 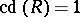implies that 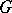is a free group (Stallings' theorem). Another subject studied are the connections between homological dimensions and other dimensions of modules and rings. E.g., the Krull dimension of a commutative ring 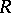coincides with 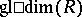if and only if all localizations of 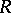by prime ideals have finite Krull dimension. Any commutative Noetherian ring 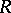for which 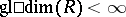is decomposable into a finite direct sum of integral domains. The local ring of a regular point is called a regular local ring in algebraic geometry. The global dimension of such a ring is identical with its Krull dimension, and also with the minimal number of generators of its maximal ideal (regular local rings are integral domains with unique prime factorization; they remain regular after localization at prime ideals).

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305
[2]	B.L. Osofsky, "Homological dimensions of modules" , Amer. Math. Soc. (1973) MR0447210 Zbl 0254.13015

Comments

For other dimensions of rings see (the editorial comments to) Dimension. Other notations for the projective and injective dimensions include projdim, pdim, injdim, idim.

References

[a1]	C. Năstăsecu, F. van Oystaeyen, "Dimensions of rings" , Reidel (1988)