Fisher-F-distribution

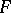-distribution, Fisher–Snedecor distribution, Snedecor distribution

A continuous probability distribution concentrated on $(0,\infty)$ with density

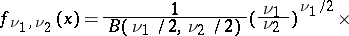(1)

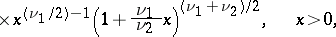where 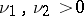are parameters, and 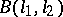is the beta-function. For 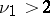it is a unimodal positive asymmetric distribution with mode at the point 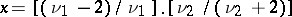. Its mathematical expectation and variance are, respectively, equal to

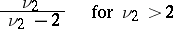and

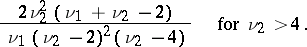The Fisher 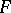-distribution reduces to a beta-distribution of the second kind (a type-VI distribution in Pearson's classification). It can be regarded as the distribution of a random variable represented in the form of the quotient

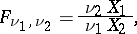where the independent random variables 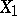and 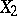have gamma-distributions (cf. Gamma-distribution) with parameters 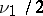and 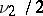, respectively. The distribution function for 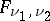can be expressed in terms of the distribution function of the beta-distribution:

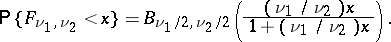(2)

This relation is used for calculating the values of the Fisher 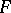-distribution by means of tables of the beta-distribution. If 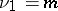and 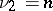are integers, then the Fisher 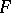-distribution with 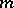and degrees of freedom is the distribution of the 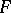-quotient

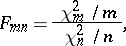(3)

where 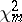and 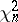are independent random variables with "chi-squared" distributions (cf. Chi-squared distribution) with 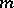and degrees of freedom, respectively.

The Fisher 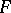-distribution plays a fundamental role in mathematical statistics and appears in the first place as the distribution of the quotient of two sample variances. Namely, let 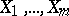and 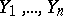be samples from normal populations with parameters 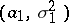and 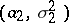. The expressions

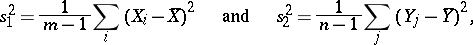where , , 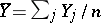serve as estimators of the variances 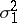and 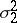. Then the so-called dispersion proportion 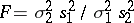has a Fisher 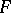-distribution with 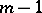and 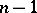degrees of freedom under the hypothesis that 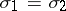(in this capacity the Fisher 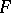-distribution is also called the distribution of the dispersion proportion). The 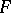-test is based on the statistic 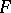, and it is used, in particular, for testing the hypothesis that the variances of two populations are equal, in the analysis of variance, regression analysis and multi-dimensional statistical analysis.

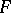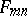The universality of the Fisher -distribution is underlined by its connections with other distributions. For the square of in (3) has a Student distribution with degrees of freedom. There are a number of approximations of the Fisher -distribution using the normal and "chi-squared" distributions.

The introduction of the Fisher 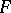-distribution in the analysis of variance is connected with the name of R.A. Fisher (1924), although Fisher himself used a quantity for the dispersion proportion, connected with 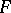by the relation 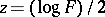. The distribution of was tabulated by Fisher, and the Fisher 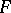-distribution by G. Snedecor (1937). At present the simpler Fisher 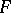-distribution is preferred, making use of its connection with the beta-distribution and tables of the incomplete beta-function.

See also Dispersion analysis; Fisher -distribution.

References

[1]	R.A. Fisher, "On a distribution yielding the error functions of several well-known statistics" , Proc. Internat. Congress mathematicians (Toronto 1924) , 2 , Univ. Toronto Press (1928) pp. 805–813
[2]	M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , 3. Design and analysis , Griffin (1969)
[3]	H. Scheffé, "The analysis of variance" , Wiley (1959)
[4]	L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)

Comments

The dispersion proportion is also known as the variance ratio, and is in the case of the 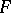-distribution also called the 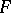-ratio. Cf. also Dispersion proportion.