Difference between revisions of "Williamson matrices"
m (link) |
m (AUTOMATIC EDIT (latexlist): Replaced 79 formulas out of 80 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 80 formulas, 79 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A [[Hadamard matrix|Hadamard matrix]] of order $n$ is an $( n \times n )$-matrix $H$ with as entries $+ 1$ and $- 1$ such that $H H ^ { T } = H ^ { T } H = n I _ { n }$, where $H ^ { T }$ is the transposed matrix of $H$ and $ { I } _ { n }$ is the unit matrix of order $n$. Note that the problem of constructing Hadamard matrices of all orders $n \equiv 0 ( \operatorname { mod } 4 )$ is as yet unsolved (1998; the first open case is $n = 428$). For a number of methods for constructing Hadamard matrices of concrete orders, see [[#References|[a1]]], [[#References|[a9]]], [[#References|[a7]]]. One of these methods, described below, is due to J. Williamson [[#References|[a10]]]. Let $A$, $B$, $C$, and $D$ be pairwise commuting symmetric [[Circulant matrix|circulant]] $( - 1 , + 1 )$-matrices of order $m$ such that $A ^ { 2 } + B ^ { 2 } + C ^ { 2 } + D ^ { 2 } = 4 m I _ { m }$ (such matrices are called Williamson matrices). Then the Williamson array | ||
| − | + | \begin{equation*} W = \left( \begin{array} { c c c c } { A } & { B } & { C } & { D } \\ { - B } & { A } & { - D } & { C } \\ { - C } & { D } & { A } & { - B } \\ { - D } & { - C } & { B } & { A } \end{array} \right) \end{equation*} | |
| − | + | is a Hadamard matrix of order $4 m$. The recent achievements about the construction of Hadamard matrices are connected with the construction of orthogonal designs [[#References|[a4]]] (cf. also [[Design with mutually orthogonal resolutions|Design with mutually orthogonal resolutions]]), Baumert–Hall arrays [[#References|[a2]]], Goethals–Seidel arrays [[#References|[a5]]] and Plotkin arrays [[#References|[a6]]], and with the construction of Williamson-type matrices, i.e., of four or eight $( - 1 , + 1 )$-matrices $\{ A _ { i } \} _ { i = 1 } ^ { k }$, $k = 4,8$, of order $m$ that satisfy the following conditions: | |
| − | + | i) $M N ^ { T } = N M ^ { T }$, $M , N \in \{ A_i \} _ { i = 1 } ^ { k }$; | |
| − | A | + | ii) $\sum _ { i = 1 } ^ { k } A _ { i } A _ { i } ^ { T } = k m I _ { m }$. Williamson-four matrices have been constructed for all orders $m \leq 40$, with the exception of $m = 35$, which was eliminated by D.Z. Djokovic [[#References|[a3]]], by means of an exhaustive computer search. It is worth mentioning that Williamson-type-four matrices of order $m = 35$ are not yet known (1998). Williamson-four and Williamson-type-four matrices are known for many values of $m$. For details, see [[#References|[a9]]], Table A1; pp. 543–547. The most recent results can be found in [[#References|[a11]]]. |
| − | + | There are known Williamson-type-eight matrices of the orders $( p + 1 ) q / 2$, where $p \equiv 1 ( \operatorname { mod } 4 )$, $q \equiv 1 ( \operatorname { mod } 4 )$ are prime numbers [[#References|[a8]]]. | |
| − | + | A set of $( - 1 , + 1 )$-matrices $\{ A _ { 1 } , \dots , A _ { k } \}$ is called a Williamson family, of type $( s _ { 1 } , \dots , s _ { k } , B _ { m } )$, if the following conditions are fulfilled: | |
| − | + | a) There exists a $( 0,1 )$-matrix $B _ { m }$ of order $m$ such that for arbitrary $i,j = 1 , \dots , k$, $A _ { i } B _ { m } A _ { j } ^ { T } = A _ { j } B _ { m } A _ { i } ^ { T }$; | |
| − | + | b) $\sum _ { i = 1 } ^ { k } s _ { i } A _ { i } A _ { i } ^ { T } = ( m \sum _ { i = 1 } ^ { k } s _ { i } ) I _ { m }$. If $s _ { 1 } = \ldots = s _ { k } = s$, then the type $( s , \dots , s , B _ { m } )$ is denoted by $( s , k , B _ { m } )$. | |
| − | If | + | If $k = 4$, $s _ { 1 } = s _ { 2 } = s _ { 3 } = s _ { 4 } = 1$, and $B _ { m } = I _ { m }$, then each Williamson family of type $( 1,1,1,1 , I _ { m } ) = ( 1,4 , I _ { m } )$ coincides with a family of Williamson-type matrices. |
| − | + | If $k = 8$, $s _ { i } = 1$ for $i = 1 , \dots , 8$, and $B _ { m } = I _ { m }$, then each Williamson family of type $( 1,1,1,1,1,1,1,1 , I _ { m } ) = ( 1,8 , I _ { m } )$ coincides with a family of Williamson-type-eight matrices. | |
| − | + | If $k = 4$, $s _ { 1 } = s _ { 2 } = s _ { 3 } = s _ { 4 } = 1$, and $B _ { m } = R$, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120210/w12021060.png"/>, | |
| − | + | \begin{equation*} r _ { i , j } = \left\{ \begin{array} { l l } { 1 , } & { \text { if } i + j = m + 1, } \\ { 0 } & { \text { otherwise, } } \end{array} \right. \end{equation*} | |
| − | + | and $A _ { i } A _ { j } = A _ { j } A _ { i }$, then each Williamson family of type $( 1,1,1,1 , R ) = ( 1,4 , R )$ coincides with a family of generalized Williamson-type matrices. | |
| − | + | An orthogonal design of order $n$ and type $( s _ { 1 } , \dots , s _ { k } )$ ($s _ { i } > 0$) on commuting variables $x _ { 1 } , \dots , x _ { k }$ is an $( n \times n )$-matrix $A$ with entries from $\{ 0 , \pm x _ { 1 } , \ldots , \pm x _ { k } \}$ such that | |
| + | |||
| + | \begin{equation*} A A ^ { T } = A ^ { T } A = \left( \sum _ { i = 1 } ^ { k } s _ { i } x _ { i } ^ { 2 } \right) I _ { n }. \end{equation*} | ||
| + | |||
| + | Let $\{ A _ { 1 } , \dots , A _ { k } \}$ be a Williamson family of type $( s _ { 1 } , \dots , s _ { k } , I _ { m } )$ and suppose there exists an orthogonal design of type $( s _ { 1 } , \dots , s _ { k } )$ and order $n$ that consists of elements $\pm x _ { i }$, $x _ { i } \neq 0$. Then there exists a Hadamard matrix of order $mn$. In other words, the existence of orthogonal designs and Williamson families implies the existence of Hadamard matrices. For more details and further constructions see [[#References|[a4]]], [[#References|[a9]]]. | ||
====References==== | ====References==== | ||
<table> | <table> | ||
| − | < | + | <tr><td valign="top">[a1]</td> <td valign="top"> S.S. Agaian, "Hadamard matrices and their applications" , ''Lecture Notes Math.'' , '''1168''' , Springer (1985) {{MR|0818740}} {{ZBL|}} </td></tr> |
| − | < | + | <tr><td valign="top">[a2]</td> <td valign="top"> L.D. Baumert, M. Hall Jr., "A new construction for Hadamard matrices" ''Bull. Amer. Math. Soc.'' , '''71''' (1965) pp. 169–170 {{MR|0169860}} {{ZBL|0156.02803}} </td></tr> |
| − | < | + | <tr><td valign="top">[a3]</td> <td valign="top"> D.Z. Djokovic, "Williamson matrices of order $4 n$ for $n = 33,35,39$" ''Discrete Math.'' , '''115''' (1993) pp. 267–271 {{MR|}} {{ZBL|0771.05024}} </td></tr> |
| − | < | + | <tr><td valign="top">[a4]</td> <td valign="top"> A.V. Geramita, J. Seberry, "Orthogonal designs: Quadratic forms and Hadamard matrices" , M. Dekker (1979) {{MR|}} {{ZBL|0411.05023}} </td></tr> |
| − | < | + | <tr><td valign="top">[a5]</td> <td valign="top"> J.M. Goethals, J.J. Seidel, "A skew–Hadamard matrix of order 36" ''J. Austral. Math. Soc. A'' , '''11''' (1970) pp. 343–344 {{MR|0269527}} {{ZBL|0226.05015}} </td></tr> |
| − | < | + | <tr><td valign="top">[a6]</td> <td valign="top"> M. Plotkin, "Decomposition of Hadamard matrices" ''J. Combin. Th. A'' , '''2''' (1972) pp. 127–130 {{MR|0300914}} {{ZBL|0241.05016}} </td></tr> |
| − | < | + | <tr><td valign="top">[a7]</td> <td valign="top"> W.D. Wallis, A.P. Street, J.S. Wallis, "Combinatorics: Room squares, sum-free sets and Hadamard matrices" , ''Lecture Notes Math.'' , '''292''' , Springer (1972) {{MR|0392580}} {{ZBL|}} </td></tr> |
| − | < | + | <tr><td valign="top">[a8]</td> <td valign="top"> J.S. Wallis, "Construction of Williamson type matrices" ''Linear and Multilinear Algebra'' , '''3''' (1975) pp. 197–207 {{MR|0396299}} {{ZBL|0321.05021}} </td></tr> |
| − | < | + | <tr><td valign="top">[a9]</td> <td valign="top"> J. Seberry, M. Yamada, "Hadamard matrices, sequences and block designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , ''Contemporary Design Theory: A Collection of Surveys'' , Wiley (1992) pp. 431–560 {{MR|1178508}} {{ZBL|0776.05028}} </td></tr> |
| − | < | + | <tr><td valign="top">[a10]</td> <td valign="top"> J. Williamson, "Hadamard's determinant theorem and the sum of four squares" ''Duke Math. J.'' , '''11''' (1944) pp. 65–81</td></tr> |
| − | < | + | <tr><td valign="top">[a11]</td> <td valign="top"> M.Y. Xia, "An infinite class of supplementary difference sets and Williamson matrices" ''J. Combin. Th. A'' , '''58''' (1991) pp. 310–317 {{MR|1129121}} {{ZBL|0758.05032}} </td></tr> |
</table> | </table> | ||
Revision as of 16:46, 1 July 2020
A Hadamard matrix of order $n$ is an $( n \times n )$-matrix $H$ with as entries $+ 1$ and $- 1$ such that $H H ^ { T } = H ^ { T } H = n I _ { n }$, where $H ^ { T }$ is the transposed matrix of $H$ and $ { I } _ { n }$ is the unit matrix of order $n$. Note that the problem of constructing Hadamard matrices of all orders $n \equiv 0 ( \operatorname { mod } 4 )$ is as yet unsolved (1998; the first open case is $n = 428$). For a number of methods for constructing Hadamard matrices of concrete orders, see [a1], [a9], [a7]. One of these methods, described below, is due to J. Williamson [a10]. Let $A$, $B$, $C$, and $D$ be pairwise commuting symmetric circulant $( - 1 , + 1 )$-matrices of order $m$ such that $A ^ { 2 } + B ^ { 2 } + C ^ { 2 } + D ^ { 2 } = 4 m I _ { m }$ (such matrices are called Williamson matrices). Then the Williamson array
\begin{equation*} W = \left( \begin{array} { c c c c } { A } & { B } & { C } & { D } \\ { - B } & { A } & { - D } & { C } \\ { - C } & { D } & { A } & { - B } \\ { - D } & { - C } & { B } & { A } \end{array} \right) \end{equation*}
is a Hadamard matrix of order $4 m$. The recent achievements about the construction of Hadamard matrices are connected with the construction of orthogonal designs [a4] (cf. also Design with mutually orthogonal resolutions), Baumert–Hall arrays [a2], Goethals–Seidel arrays [a5] and Plotkin arrays [a6], and with the construction of Williamson-type matrices, i.e., of four or eight $( - 1 , + 1 )$-matrices $\{ A _ { i } \} _ { i = 1 } ^ { k }$, $k = 4,8$, of order $m$ that satisfy the following conditions:
i) $M N ^ { T } = N M ^ { T }$, $M , N \in \{ A_i \} _ { i = 1 } ^ { k }$;
ii) $\sum _ { i = 1 } ^ { k } A _ { i } A _ { i } ^ { T } = k m I _ { m }$. Williamson-four matrices have been constructed for all orders $m \leq 40$, with the exception of $m = 35$, which was eliminated by D.Z. Djokovic [a3], by means of an exhaustive computer search. It is worth mentioning that Williamson-type-four matrices of order $m = 35$ are not yet known (1998). Williamson-four and Williamson-type-four matrices are known for many values of $m$. For details, see [a9], Table A1; pp. 543–547. The most recent results can be found in [a11].
There are known Williamson-type-eight matrices of the orders $( p + 1 ) q / 2$, where $p \equiv 1 ( \operatorname { mod } 4 )$, $q \equiv 1 ( \operatorname { mod } 4 )$ are prime numbers [a8].
A set of $( - 1 , + 1 )$-matrices $\{ A _ { 1 } , \dots , A _ { k } \}$ is called a Williamson family, of type $( s _ { 1 } , \dots , s _ { k } , B _ { m } )$, if the following conditions are fulfilled:
a) There exists a $( 0,1 )$-matrix $B _ { m }$ of order $m$ such that for arbitrary $i,j = 1 , \dots , k$, $A _ { i } B _ { m } A _ { j } ^ { T } = A _ { j } B _ { m } A _ { i } ^ { T }$;
b) $\sum _ { i = 1 } ^ { k } s _ { i } A _ { i } A _ { i } ^ { T } = ( m \sum _ { i = 1 } ^ { k } s _ { i } ) I _ { m }$. If $s _ { 1 } = \ldots = s _ { k } = s$, then the type $( s , \dots , s , B _ { m } )$ is denoted by $( s , k , B _ { m } )$.
If $k = 4$, $s _ { 1 } = s _ { 2 } = s _ { 3 } = s _ { 4 } = 1$, and $B _ { m } = I _ { m }$, then each Williamson family of type $( 1,1,1,1 , I _ { m } ) = ( 1,4 , I _ { m } )$ coincides with a family of Williamson-type matrices.
If $k = 8$, $s _ { i } = 1$ for $i = 1 , \dots , 8$, and $B _ { m } = I _ { m }$, then each Williamson family of type $( 1,1,1,1,1,1,1,1 , I _ { m } ) = ( 1,8 , I _ { m } )$ coincides with a family of Williamson-type-eight matrices.
If $k = 4$, $s _ { 1 } = s _ { 2 } = s _ { 3 } = s _ { 4 } = 1$, and $B _ { m } = R$, 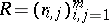 ,
,
\begin{equation*} r _ { i , j } = \left\{ \begin{array} { l l } { 1 , } & { \text { if } i + j = m + 1, } \\ { 0 } & { \text { otherwise, } } \end{array} \right. \end{equation*}
and $A _ { i } A _ { j } = A _ { j } A _ { i }$, then each Williamson family of type $( 1,1,1,1 , R ) = ( 1,4 , R )$ coincides with a family of generalized Williamson-type matrices.
An orthogonal design of order $n$ and type $( s _ { 1 } , \dots , s _ { k } )$ ($s _ { i } > 0$) on commuting variables $x _ { 1 } , \dots , x _ { k }$ is an $( n \times n )$-matrix $A$ with entries from $\{ 0 , \pm x _ { 1 } , \ldots , \pm x _ { k } \}$ such that
\begin{equation*} A A ^ { T } = A ^ { T } A = \left( \sum _ { i = 1 } ^ { k } s _ { i } x _ { i } ^ { 2 } \right) I _ { n }. \end{equation*}
Let $\{ A _ { 1 } , \dots , A _ { k } \}$ be a Williamson family of type $( s _ { 1 } , \dots , s _ { k } , I _ { m } )$ and suppose there exists an orthogonal design of type $( s _ { 1 } , \dots , s _ { k } )$ and order $n$ that consists of elements $\pm x _ { i }$, $x _ { i } \neq 0$. Then there exists a Hadamard matrix of order $mn$. In other words, the existence of orthogonal designs and Williamson families implies the existence of Hadamard matrices. For more details and further constructions see [a4], [a9].
References
| [a1] | S.S. Agaian, "Hadamard matrices and their applications" , Lecture Notes Math. , 1168 , Springer (1985) MR0818740 |
| [a2] | L.D. Baumert, M. Hall Jr., "A new construction for Hadamard matrices" Bull. Amer. Math. Soc. , 71 (1965) pp. 169–170 MR0169860 Zbl 0156.02803 |
| [a3] | D.Z. Djokovic, "Williamson matrices of order $4 n$ for $n = 33,35,39$" Discrete Math. , 115 (1993) pp. 267–271 Zbl 0771.05024 |
| [a4] | A.V. Geramita, J. Seberry, "Orthogonal designs: Quadratic forms and Hadamard matrices" , M. Dekker (1979) Zbl 0411.05023 |
| [a5] | J.M. Goethals, J.J. Seidel, "A skew–Hadamard matrix of order 36" J. Austral. Math. Soc. A , 11 (1970) pp. 343–344 MR0269527 Zbl 0226.05015 |
| [a6] | M. Plotkin, "Decomposition of Hadamard matrices" J. Combin. Th. A , 2 (1972) pp. 127–130 MR0300914 Zbl 0241.05016 |
| [a7] | W.D. Wallis, A.P. Street, J.S. Wallis, "Combinatorics: Room squares, sum-free sets and Hadamard matrices" , Lecture Notes Math. , 292 , Springer (1972) MR0392580 |
| [a8] | J.S. Wallis, "Construction of Williamson type matrices" Linear and Multilinear Algebra , 3 (1975) pp. 197–207 MR0396299 Zbl 0321.05021 |
| [a9] | J. Seberry, M. Yamada, "Hadamard matrices, sequences and block designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 431–560 MR1178508 Zbl 0776.05028 |
| [a10] | J. Williamson, "Hadamard's determinant theorem and the sum of four squares" Duke Math. J. , 11 (1944) pp. 65–81 |
| [a11] | M.Y. Xia, "An infinite class of supplementary difference sets and Williamson matrices" J. Combin. Th. A , 58 (1991) pp. 310–317 MR1129121 Zbl 0758.05032 |
Williamson matrices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Williamson_matrices&oldid=37538