Difference between revisions of "Kronecker symbol"
(TeX partially done) |
(TeX partially done) |
||
| Line 7: | Line 7: | ||
$i,j = 1,2,\ldots$. When $1 \le i,j \le n$, the Kronecker symbol $\delta^i_j$ has $n^2$ components, and the matrix $(\delta^i_j)$ is the [[unit matrix]]. The Kronecker symbol was first used by L. Kronecker (1866). | $i,j = 1,2,\ldots$. When $1 \le i,j \le n$, the Kronecker symbol $\delta^i_j$ has $n^2$ components, and the matrix $(\delta^i_j)$ is the [[unit matrix]]. The Kronecker symbol was first used by L. Kronecker (1866). | ||
| − | The Kronecker symbol may be generalized, considering instead a set of quantities $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ with $2p$ integer (upper and lower) indices, $i_\alpha\,,j_\beta = 1,\ldots,n$, equal to $+1$ (or $-1$) if the sequence $(i_1\ldots i_p)$ is an even (odd) permutation of the distinct indices $(j_1\ldots j_p)$ and zero otherwise. The numbers $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ (when $p \ge 2$ often denoted by $\epsilon^{i_1\ldots i_p}_{j_1\ldots j_p}$) are called the ''components'' of the Kronecker symbol. An [[affine tensor]] of type $(p,p)$ whose components relative to some basis are equal to the components of the Kronecker symbol has the same components relative to any other basis. | + | The Kronecker symbol may be generalized, considering instead a set of quantities $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ with $2p$ integer (upper and lower) indices, $i_\alpha\,,j_\beta = 1,\ldots,n$, equal to $+1$ (or $-1$) if the sequence $(i_1\ldots i_p)$ is an even (odd) permutation of the distinct indices $(j_1\ldots j_p)$ and zero otherwise. The numbers $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ (when $p \ge 2$ often denoted by $\epsilon^{i_1\ldots i_p}_{j_1\ldots j_p}$) are called the ''components'' of the Kronecker symbol. An [[affine tensor]] of type $(p,p)$ whose components relative to some basis are equal to the components of the Kronecker symbol is ''isotropic'': has the same components relative to any other basis. |
The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant | The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant | ||
| − | + | $$ | |
| − | + | \left|{ | |
| − | + | \begin{array}{ccc} a^1_1 & \ldots & a^1_n \\ \vdots & \ddots & \vdots \\ a^n_1 & \ldots & a^n_n \end{array} | |
| + | }\right| | ||
| + | $$ | ||
is equal to the sum | is equal to the sum | ||
| − | + | $$ | |
| − | + | \sum \delta^{i_1\ldots i_n}_{1\ldots n} a^1_{i_1} \cdots a^n_{i_n} | |
| − | + | $$ | |
| − | where the summation is performed over all | + | where the summation is performed over all $n!$ permutations $( i_1\ldots i_n )$of the numbers $\{1,\ldots, n \$. The ''alternant'' of the tensor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055900/k05590024.png" /> is given by |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055900/k05590025.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055900/k05590025.png" /></td> </tr></table> | ||
Revision as of 19:26, 13 January 2016
Kronecker delta
The number $\delta^i_j$ defined by $$ \delta^i_j = \begin{cases} 1 & \text{if}\, i = j \\ 0 & \text{if}\, i \ne j \end{cases}\ \ , $$ $i,j = 1,2,\ldots$. When $1 \le i,j \le n$, the Kronecker symbol $\delta^i_j$ has $n^2$ components, and the matrix $(\delta^i_j)$ is the unit matrix. The Kronecker symbol was first used by L. Kronecker (1866).
The Kronecker symbol may be generalized, considering instead a set of quantities $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ with $2p$ integer (upper and lower) indices, $i_\alpha\,,j_\beta = 1,\ldots,n$, equal to $+1$ (or $-1$) if the sequence $(i_1\ldots i_p)$ is an even (odd) permutation of the distinct indices $(j_1\ldots j_p)$ and zero otherwise. The numbers $\delta^{i_1\ldots i_p}_{j_1\ldots j_p}$ (when $p \ge 2$ often denoted by $\epsilon^{i_1\ldots i_p}_{j_1\ldots j_p}$) are called the components of the Kronecker symbol. An affine tensor of type $(p,p)$ whose components relative to some basis are equal to the components of the Kronecker symbol is isotropic: has the same components relative to any other basis.
The Kronecker symbol is convenient in various problems of tensor calculus. For example, the determinant
$$
\left|{
\begin{array}{ccc} a^1_1 & \ldots & a^1_n \\ \vdots & \ddots & \vdots \\ a^n_1 & \ldots & a^n_n \end{array}
}\right|
$$
is equal to the sum
$$
\sum \delta^{i_1\ldots i_n}_{1\ldots n} a^1_{i_1} \cdots a^n_{i_n}
$$
where the summation is performed over all $n!$ permutations $( i_1\ldots i_n )$of the numbers $\{1,\ldots, n \$. The alternant of the tensor  is given by
is given by
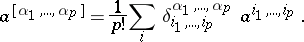 |
References
| [1] | L. Kronecker, "Vorlesungen über die Theorie der Determinanten" , Leipzig (1903) |
Comment
For the Kronecker symbol in number theory, see Legendre–Jacobi–Kronecker symbol
Kronecker symbol. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker_symbol&oldid=37518