Difference between revisions of "Triangular norm"
(→References: expand bibliodata) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
''t-norm'' | ''t-norm'' | ||
| − | A binary operation on the unit interval | + | A [[binary operation]] on the unit interval $[0,1]$, i.e., a function $T : [0,1]^2 \rightarrow [0,1]$ such that for all $x,y,z \in [0,1]$ the following four axioms are satisfied: |
| − | T1) (commutativity) | + | T1) (commutativity) $T(x,y) = T(y,x)$; |
| − | T2) (associativity) | + | T2) (associativity) $T(x,T(y,z)) = T(T(x,y),z)$; |
| − | T3) (monotonicity) | + | T3) (monotonicity) $T(x,y) \le T(x,z)$ whenever $y \le z$; |
| − | T4) (boundary condition) | + | T4) (boundary condition) $T(x,1) = x$. |
| − | If | + | If $T$ is a triangular norm, then its ''dual triangular co-norm'' $S$ is given by |
| + | $$ | ||
| + | S(x,y) = 1 - T(1-x,1-y) \ . | ||
| + | $$ | ||
| − | + | A function $T : [0,1]^2 \rightarrow [0,1]$ is a triangular norm if and only if $([0,1], T, {\le})$ is a fully ordered commutative [[semi-group]] (cf. [[#References|[a3]]] and [[O-group|$o$-group]]) with neutral element $1$ and annihilator $0$, where ${\le}$ is the usual order on $[0,1]$. | |
| − | + | For each $I$-semi-group $([a,b],{\star})$, i.e. a semi-group in which the binary associative operation $\star$ on the closed subinterval $[a,b]$ of the extended real line is continuous and one of the boundary points of $[a,b]$ acts as a neutral element and the other one as an annihilator ([[#References|[a6]]], [[#References|[a7]]]), there exists a continuous triangular norm $T$ or a continuous triangular co-norm $S$ such that the linear transformation $\phi : [a,b] \rightarrow [0,1]$ given by | |
| − | + | $$ | |
| − | + | \phi : x \mapsto \frac{x-a}{b-a} | |
| − | + | $$ | |
| − | + | is an [[Isomorphism|isomorphism]] between $([a,b],{\star})$ and either $([0,1],T)$ or $([0,1],S)$. | |
| − | |||
| − | is an [[Isomorphism|isomorphism]] between | ||
The following are the four basic triangular norms, together with their dual triangular co-norms: | The following are the four basic triangular norms, together with their dual triangular co-norms: | ||
| Line 84: | Line 85: | ||
<TR><TD valign="top">[a9]</TD> <TD valign="top"> B. Schweizer, A. Sklar, "Probabilistic metric spaces" , North-Holland (1983)</TD></TR> | <TR><TD valign="top">[a9]</TD> <TD valign="top"> B. Schweizer, A. Sklar, "Probabilistic metric spaces" , North-Holland (1983)</TD></TR> | ||
</table> | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 18:51, 27 December 2015
t-norm
A binary operation on the unit interval $[0,1]$, i.e., a function $T : [0,1]^2 \rightarrow [0,1]$ such that for all $x,y,z \in [0,1]$ the following four axioms are satisfied:
T1) (commutativity) $T(x,y) = T(y,x)$;
T2) (associativity) $T(x,T(y,z)) = T(T(x,y),z)$;
T3) (monotonicity) $T(x,y) \le T(x,z)$ whenever $y \le z$;
T4) (boundary condition) $T(x,1) = x$.
If $T$ is a triangular norm, then its dual triangular co-norm $S$ is given by $$ S(x,y) = 1 - T(1-x,1-y) \ . $$
A function $T : [0,1]^2 \rightarrow [0,1]$ is a triangular norm if and only if $([0,1], T, {\le})$ is a fully ordered commutative semi-group (cf. [a3] and $o$-group) with neutral element $1$ and annihilator $0$, where ${\le}$ is the usual order on $[0,1]$.
For each $I$-semi-group $([a,b],{\star})$, i.e. a semi-group in which the binary associative operation $\star$ on the closed subinterval $[a,b]$ of the extended real line is continuous and one of the boundary points of $[a,b]$ acts as a neutral element and the other one as an annihilator ([a6], [a7]), there exists a continuous triangular norm $T$ or a continuous triangular co-norm $S$ such that the linear transformation $\phi : [a,b] \rightarrow [0,1]$ given by $$ \phi : x \mapsto \frac{x-a}{b-a} $$ is an isomorphism between $([a,b],{\star})$ and either $([0,1],T)$ or $([0,1],S)$.
The following are the four basic triangular norms, together with their dual triangular co-norms:
i) the minimum 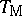 and maximum
and maximum 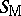 , given by
, given by
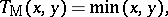 |
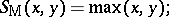 |
ii) the product 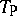 and probabilistic sum
and probabilistic sum 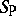 , given by
, given by
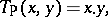 |
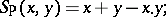 |
iii) the Lukasiewicz triangular norm 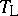 and Lukasiewicz triangular co-norm
and Lukasiewicz triangular co-norm 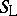 , given by
, given by
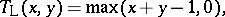 |
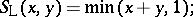 |
iv) the weakest triangular norm (or drastic product) 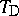 and strongest triangular co-norm
and strongest triangular co-norm 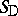 , given by
, given by
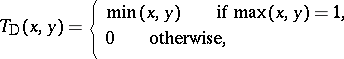 |
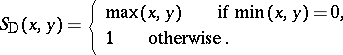 |
Let  be a family of triangular norms and let
be a family of triangular norms and let 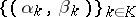 be a family of pairwise disjoint open subintervals of the unit interval
be a family of pairwise disjoint open subintervals of the unit interval 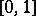 (i.e.,
(i.e.,  is an at most countable index set). Consider the linear transformations
is an at most countable index set). Consider the linear transformations 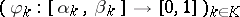 given by
given by
 |
Then the function 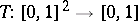 defined by
defined by
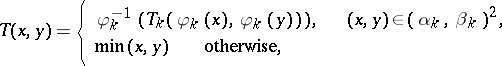 |
is a triangular norm, which is called the ordinal sum of the summands 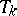 ,
,  .
.
The following representations hold ([a1], [a5], [a6]):
A function 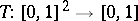 is a continuous Archimedean triangular norm, i.e., for all
is a continuous Archimedean triangular norm, i.e., for all 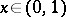 one has
one has 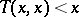 , if and only if there exists a continuous, strictly decreasing function
, if and only if there exists a continuous, strictly decreasing function 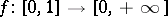 with
with 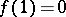 such that for all
such that for all 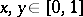 ,
,
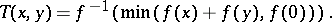 |
The function 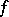 is then called an additive generator of
is then called an additive generator of 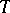 ; it is uniquely determined by
; it is uniquely determined by  up to a positive multiplicative constant.
up to a positive multiplicative constant.
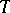 is a continuous triangular norm if and only if
is a continuous triangular norm if and only if 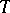 is an ordinal sum whose summands are continuous Archimedean triangular norms.
is an ordinal sum whose summands are continuous Archimedean triangular norms.
Triangular norms are applied in many fields, such as probabilistic metric spaces [a9], [a4], fuzzy sets, fuzzy logics and their applications [a4], the theory of generalized measures [a2], [a8], functional equations [a1] and in non-linear differential and difference equations (see [a4], [a8]).
References
| [a1] | J. Aczél, "Lectures on functional equations and their applications" , Acad. Press (1969) |
| [a2] | D. Butnariu, E.P. Klement, "Triangular norm-based measures and games with fuzzy coalitions" , Kluwer Acad. Publ. (1993) |
| [a3] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) Zbl 0137.02001 |
| [a4] | E.P. Klement, R. Mesiar, E. Pap, "Triangular norms" Trends in Logic--Studia Logica Library 8 Kluwer Academic ISBN 0-7923-6416-3 Zbl 0972.03002 |
| [a5] | C.M. Ling, "Representation of associative functions" Publ. Math. Debrecen , 12 (1965) pp. 189–212 |
| [a6] | P.S. Mostert, A.L. Shields, "On the structure of semigroups on a compact manifold with boundary" Ann. of Math. , 65 (1957) pp. 117–143 |
| [a7] | A.B. Paalman-de Miranda, "Topological semigroups" , Tracts , 11 , Math. Centre Amsterdam (1970) |
| [a8] | E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995) |
| [a9] | B. Schweizer, A. Sklar, "Probabilistic metric spaces" , North-Holland (1983) |
Triangular norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triangular_norm&oldid=37115