Difference between revisions of "Enumeration theory"
m (better) |
(TeX partially done) |
||
| Line 54: | Line 54: | ||
$$ | $$ | ||
| − | If | + | If $X=B$, then $R(B)$ is isomorphic to the algebra of exponential power series |
| + | $$ | ||
| + | \sum_{k=0}^\infty a_k \frac{x^k}{k!} | ||
| + | $$ | ||
| + | and $\zeta \leftrightarrow e^x$, $\mu \leftrightarrow e^{-x}$, where $[x,y] \sim [u,v]$ for $|y \setminus x| = |v \setminus u|$. | ||
| − | + | If $X = D$ and one considers $[x,y] \sim [u,v]$ for $v/u = y/x$, then $R(d)$ is isomorphic to the algebra of [[formal Dirichlet series]] and | |
| + | $$ | ||
| + | \zeta \leftrightarrow \zeta(s) = \sum{n=1}^\infty \frac{1}{n^s}\ ,\ \ \mu \leftrightarrow \frac{1}{\zeta(s)} = \sum_{n=1}^\infty \frac{\mu(n)}{n^s}\ . | ||
| + | $$ | ||
| − | + | Example. Let $c(x,y)$ be the number of chains of the form $x < z_1 < z_2 < \cdots < z_{l-1} < y$ in $X$, then $(\zeta-\delta)^k(x,y)$ is the number of such chains of length $k$ (i.e. $l=k$), hence | |
| − | + | $$ | |
| − | + | c(x,y) = \sum_{k=0}^\infty (\zeta-\delta)^k(x,y) = [\delta-(\zeta-\delta]^{-1}(x,y) = (2\delta-\zeta)^{-1}(x,y)\ . | |
| − | + | $$ | |
| − | |||
| − | |||
| − | Example. Let | ||
| − | |||
| − | |||
| − | |||
| − | |||
Consider this formula in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583079.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583080.png" />. In the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583081.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583082.png" />, the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583083.png" /> is the number of ordered decompositions (partitions) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583084.png" />. In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583085.png" />, the formula takes the form | Consider this formula in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583079.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583080.png" />. In the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583081.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583082.png" />, the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583083.png" /> is the number of ordered decompositions (partitions) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583084.png" />. In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035830/e03583085.png" />, the formula takes the form | ||
Revision as of 12:42, 20 December 2015
The branch of combinatorial analysis in which one examines and develops methods for solving enumeration problems (cf. Enumeration problem). The problems usually amount to counting the number of elements in a finite set having certain properties, or else their equivalence classes. The methods include, for example, the inclusion-and-exclusion principle and various generalizations of it. Pólya's enumeration theory (see Pólya theorem) frequently enables one to overcome difficulties in counting various objects when these are to be considered as indistinguishable. A basic tool in enumeration problems is provided by generating functions (cf. Generating function); they also play an important part in obtaining asymptotic relations (cf. [1]–[3]).
To obtain generating functions in combinatorics considerable use is made of algebras of formal power series and of various symbolic methods (cf. [1], [2], [4]). The basis of the general approach to developing methods for obtaining generating functions is the fact that many discrete objects have a natural order (cf. [1], [5]). In what follows, constructions of incidence algebras are given as examples and it is shown how they enable one to solve certain enumeration problems.
Suppose one is given a partially ordered set $X$ with locally finite order relation $\le$, and suppose that $\le$ is locally finite, i.e. suppose that any segment $$ [a,b] = \{ x \in X : a \le x \ \wedge\ x \le b \} $$ is finite.
The incidence algebra $I(X)$ is the set of functions $f(x,y)$, $x,y \in X$, that take real values and are such that $f(x,y) = 0$ unless $x \le y$. The sum of two such functions and multiplication by a number are defined in the usual way, while the product $f \star g = h$ is introduced via $$ h(x,y) = \sum_{z \in [x,y]} f(x,z) g(z,y) \ . $$ Multiplication is associative and distributive with respect to addition. The algebra $I(X)$ has unit $$ \delta = \delta(x,y) = \begin{cases} 1 & \text{if}\,x = y \\ 0 & \text{if}\,x \ne y \end{cases} \ . $$
Two elements are distinguished in $I(X)$: the zeta-function $$ \zeta(x,y) = \begin{cases} 1 & \text{if}\,x \le y \\ 0 & \text{otherwise} \end{cases} $$ and the Möbius function $\mu(x,y)$, which is its inverse. The following statement holds: If a locally finite partially ordered set $X$ contains its own greatest lower bound, if a function $f(x)$ is defined for all $x \in X$ and if $g(x) = \sum_{y \le x} f(x)$ for all $x \in x$, then for all $x \in X$, $$ f(x) = \sum_{y \le x} g(y) \mu(y,x) $$ (Möbius' inversion theorem).
If $X = B$ is the set of all finite subsets of a certain countable set, and if $x \le y$ means that $x \subseteq y$, then for $x \le y$ $$ \mu_B(x,y) = (-1)^{|y|-|x|} $$ and Möbius inversion is simply the inclusion-and-exclusion principle.
If $X = D$ is a set of natural numbers and $x \le y$ means that $x$ divides $y$, then for $x \le y$ one has $\mu_D(x,y) = \mu(y/x)$, where $\mu$ is the number-theoretic Möbius function.
A reduced incidence algebra $R(X)$ is a subalgebra of $I(X)$ that contains all functions of $I(X)$ that take equal values on equivalent segments. The relation of segment equivalence has the property that if $f(x,y) = f(u,v)$ and $g(x,y) = g(u,v)$ for $[x,y] \sim [u,v]$, then also $f \star g (x,y) = f \star g (u,v)$.
This is true, for example, if isomorphic segments are taken as equivalent. The zeta-function and the Möbius function always belong to $R(X)$.
If $X = \mathbf{N}_0 = \{0,1,2,\ldots \}$ with the natural ordering of numbers, then $I(\mathbf{N}_0)$ is isomorphic to the algebra of upper-triangular infinite matrices. If $R(\mathbf{N}_0)$ consists of all functions $f \in I(\mathbf{N}_0)$ for which $f(m,n) = f(m',n')$ for $n - m = n' - m' = k$, then the one-to-one relation $$ f \leftrightarrow \sum_{k=0}^\infty a_k x^k\ ,\ \ g \leftrightarrow \sum_{k=0}^\infty b_k x^k $$ holds, where $a_k = f(m,n)$ and $b_k = g(m,n)$ for $k = n-m$; thus $$ f \star g \leftrightarrow \sum_{k=0}^\infty c_k x^k\ ,\ \ c_k = \sum_{s=0}^k a+s b_{k-s} \ . $$
Hence $R(\mathbf{N}_0)$ is isomorphic to the algebra of formal power series and $$ \zeta \leftrightarrow (1-x)^{-1}\ ,\ \ \mu \leftrightarrow (1-x) \ . $$
If $X=B$, then $R(B)$ is isomorphic to the algebra of exponential power series $$ \sum_{k=0}^\infty a_k \frac{x^k}{k!} $$ and $\zeta \leftrightarrow e^x$, $\mu \leftrightarrow e^{-x}$, where $[x,y] \sim [u,v]$ for $|y \setminus x| = |v \setminus u|$.
If $X = D$ and one considers $[x,y] \sim [u,v]$ for $v/u = y/x$, then $R(d)$ is isomorphic to the algebra of formal Dirichlet series and $$ \zeta \leftrightarrow \zeta(s) = \sum{n=1}^\infty \frac{1}{n^s}\ ,\ \ \mu \leftrightarrow \frac{1}{\zeta(s)} = \sum_{n=1}^\infty \frac{\mu(n)}{n^s}\ . $$
Example. Let $c(x,y)$ be the number of chains of the form $x < z_1 < z_2 < \cdots < z_{l-1} < y$ in $X$, then $(\zeta-\delta)^k(x,y)$ is the number of such chains of length $k$ (i.e. $l=k$), hence $$ c(x,y) = \sum_{k=0}^\infty (\zeta-\delta)^k(x,y) = [\delta-(\zeta-\delta]^{-1}(x,y) = (2\delta-\zeta)^{-1}(x,y)\ . $$
Consider this formula in 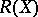 for
for 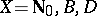 . In the case
. In the case 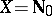 and
and 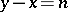 , the number
, the number 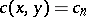 is the number of ordered decompositions (partitions) of
is the number of ordered decompositions (partitions) of  . In
. In 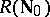 , the formula takes the form
, the formula takes the form
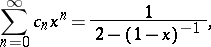 |
hence 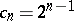 ,
, 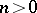 .
.
In the case 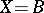 , the number
, the number 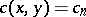 is the number of ordered decompositions of an
is the number of ordered decompositions of an  -element set,
-element set, 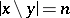 , and
, and
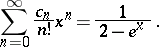 |
In the case 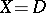 , the number
, the number 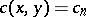 is the number of ordered decompositions of
is the number of ordered decompositions of 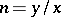 into factors, hence
into factors, hence
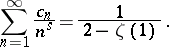 |
References
| [1] | V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [2] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
| [3] | , Enumeration problems in combinatorial analysis , Moscow (1979) (In Russian; translated from English) |
| [4] | R. Mullin, G.-C. Rota, "On the foundations of combinatorial theory: III. Theory of binomial enumeration" B. Harris (ed.) , Graph theory and its applications , Acad. Press (1970) pp. 167–213 |
| [5] | G.-C. Rota, "On the foundations of combinatorial theory: I. Theory of Möbius functions" Z. Wahrscheinlichkeitstheor. Verw. Geb. , 2 : 4 (1964) pp. 340–368 |
| [6] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
Enumeration theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enumeration_theory&oldid=37015