|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304901.png" /> be a finite [[Partially ordered set|partially ordered set]] (abbreviated: poset) which possesses a rank function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304902.png" />, i.e. a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304903.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304904.png" /> for some minimal element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304905.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304906.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304907.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304908.png" /> covers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s1304909.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049010.png" /> and there is no element between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049012.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049013.png" /> be its <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049014.png" />th level and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049015.png" /> be the rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049016.png" />.
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | An [[anti-chain]] or Sperner family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049017.png" /> is a subset of pairwise incomparable elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049018.png" />. Obviously, each level is an anti-chain. The [[width of a partially ordered set]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049019.png" /> (Dilworth number or Sperner number) is the maximum size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049020.png" /> of an anti-chain of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049021.png" />. The poset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049022.png" /> is said to have the Sperner property if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049023.png" />. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also [[Sperner theorem|Sperner theorem]]).
| + | Out of 67 formulas, 65 were replaced by TEX code.--> |
| | | | |
| − | More generally, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049025.png" />-family, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049026.png" />, is a subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049027.png" /> containing no chain of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049028.png" /> elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049029.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049030.png" /> has the strong Sperner property if for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049031.png" /> the largest size of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049032.png" />-family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049033.png" /> equals the largest size of a union of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049034.png" /> levels. There exist several classes of posets having the strong Sperner property:
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | Let $P$ be a finite [[Partially ordered set|partially ordered set]] (abbreviated: poset) which possesses a rank function $r$, i.e. a function $r : P \rightarrow \mathbf{N}$ such that $r ( p ) = 0$ for some minimal element $p$ of $P$ and $r ( q ) = r ( p ) + 1$ whenever $q$ covers $p$, i.e. $p < q$ and there is no element between $p$ and $q$. Let $N _ { k } : = \{ p \in P : r ( p ) = k \}$ be its $k$th level and let $r ( P ) : = \operatorname { max } \{ r ( p ) : p \in P \}$ be the rank of $P$. |
| | | | |
| − | LYM posets, i.e. posets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049035.png" /> satisfying the LYM inequality (cf. also [[Sperner theorem|Sperner theorem]])
| + | An [[anti-chain]] or Sperner family in $P$ is a subset of pairwise incomparable elements of $P$. Obviously, each level is an anti-chain. The [[width of a partially ordered set]] $P$ (Dilworth number or Sperner number) is the maximum size $d ( P )$ of an anti-chain of $P$. The poset $P$ is said to have the Sperner property if $d ( P ) = \operatorname { max } _ { k } | N _ { k } |$. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also [[Sperner theorem|Sperner theorem]]). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049036.png" /></td> </tr></table>
| + | More generally, a $k$-family, $ k = 1 , \ldots , r ( P )$, is a subset of $P$ containing no chain of $k + 1$ elements in $P$, and $P$ has the strong Sperner property if for each $k$ the largest size of a $k$-family in $P$ equals the largest size of a union of $k$ levels. There exist several classes of posets having the strong Sperner property: |
| | | | |
| − | for every anti-chain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049037.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049038.png" /> or, equivalently,
| + | LYM posets, i.e. posets $P$ satisfying the LYM inequality (cf. also [[Sperner theorem|Sperner theorem]]) |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049039.png" /></td> </tr></table>
| + | \begin{equation*} \sum _ { k = 0 } ^ { r ( P ) } \frac { | \mathcal{F} \cap N _ { k } | } { | N _ { k } | } \leq 1 \end{equation*} |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049041.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049042.png" />. This equivalent property is called the normalized matching property of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049043.png" />. | + | for every anti-chain $\mathcal{F}$ in $P$ or, equivalently, |
| | | | |
| − | Symmetric chain orders, i.e. ranked posets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049044.png" /> which can be decomposed into chains of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049045.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049047.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049048.png" />.
| + | \begin{equation*} \frac { | \nabla ( {\cal A} ) | } { | N _ { k + 1} | } \geq \frac { | {\cal A} | } { | N _ { k } | } \end{equation*} |
| | | | |
| − | Peck posets, i.e. ranked posets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049049.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049050.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049051.png" /> and there is a linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049052.png" /> on the vector space having the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049053.png" /> with the following properties:
| + | for all $A \subseteq N _ { k }$, $k = 0 , \ldots , r ( P ) - 1$, where $\nabla ( \mathcal{A} ) : = \{ q \in N _ { k + 1} : q > p \ \text { for some } p \in \mathcal{A} \}$. This equivalent property is called the normalized matching property of $P$. |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049054.png" /> with some numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049055.png" />,
| + | Symmetric chain orders, i.e. ranked posets $P$ which can be decomposed into chains of the form $( p _ { 0 } < \ldots < p _ { h } )$ where $r ( p _ { i } ) = r ( p _ { 0 } ) + i$, $i = 0 , \ldots , h$, and $r ( p _ { 0 } ) + r ( p _ { h } ) = r ( P )$. |
| | | | |
| − | the subspace generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049056.png" /> is mapped via <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049057.png" /> to a subspace of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049058.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049059.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049061.png" /> are posets from one class, then also the direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049062.png" /> (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049063.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049064.png" /> (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
| + | Peck posets, i.e. ranked posets $P$ such that $| N _ { k } | = | N _ { r \langle P \rangle -k } |$ for all $k$ and there is a linear operator $\tilde { \nabla }$ on the vector space having the basis $\{ \tilde{p} : p \in P \}$ with the following properties: |
| | | | |
| − | Every LYM poset with the symmetry and unimodality property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049065.png" /> is a symmetric chain order and every symmetric chain order is a Peck poset.
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049054.png"/> with some numbers $c ( p , q )$, |
| | | | |
| − | Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049066.png" />-dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049067.png" />-dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049068.png" /> is sufficiently large. | + | the subspace generated by $\{ \tilde { p } : p \in N _ { i } \}$ is mapped via $\widetilde { \nabla } ^ { j - i }$ to a subspace of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130490/s13049058.png"/> for all $0 \leq i < j \leq r ( P )$. If $P$ and $Q$ are posets from one class, then also the direct product $P \times Q$ (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: $| N _ { k } | ^ { 2 } \geq | N _ { k - 1} | | N _ { k + 1}|$ for all $k$ (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets. |
| | + | |
| | + | Every LYM poset with the symmetry and unimodality property $| N _ { 0 } | = | N _ { r(P) } | \leq | N _ { 1 } | = | N _ { r ( P ) - 1} | \leq \dots$ is a symmetric chain order and every symmetric chain order is a Peck poset. |
| | + | |
| | + | Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an $n$-dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an $n$-dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if $n$ is sufficiently large. |
| | | | |
| | Details can be found in [[#References|[a1]]]. | | Details can be found in [[#References|[a1]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Engel, "Sperner theory" , Cambridge Univ. Press (1997)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> K. Engel, "Sperner theory" , Cambridge Univ. Press (1997)</td></tr></table> |
Let $P$ be a finite partially ordered set (abbreviated: poset) which possesses a rank function $r$, i.e. a function $r : P \rightarrow \mathbf{N}$ such that $r ( p ) = 0$ for some minimal element $p$ of $P$ and $r ( q ) = r ( p ) + 1$ whenever $q$ covers $p$, i.e. $p < q$ and there is no element between $p$ and $q$. Let $N _ { k } : = \{ p \in P : r ( p ) = k \}$ be its $k$th level and let $r ( P ) : = \operatorname { max } \{ r ( p ) : p \in P \}$ be the rank of $P$.
An anti-chain or Sperner family in $P$ is a subset of pairwise incomparable elements of $P$. Obviously, each level is an anti-chain. The width of a partially ordered set $P$ (Dilworth number or Sperner number) is the maximum size $d ( P )$ of an anti-chain of $P$. The poset $P$ is said to have the Sperner property if $d ( P ) = \operatorname { max } _ { k } | N _ { k } |$. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also Sperner theorem).
More generally, a $k$-family, $ k = 1 , \ldots , r ( P )$, is a subset of $P$ containing no chain of $k + 1$ elements in $P$, and $P$ has the strong Sperner property if for each $k$ the largest size of a $k$-family in $P$ equals the largest size of a union of $k$ levels. There exist several classes of posets having the strong Sperner property:
LYM posets, i.e. posets $P$ satisfying the LYM inequality (cf. also Sperner theorem)
\begin{equation*} \sum _ { k = 0 } ^ { r ( P ) } \frac { | \mathcal{F} \cap N _ { k } | } { | N _ { k } | } \leq 1 \end{equation*}
for every anti-chain $\mathcal{F}$ in $P$ or, equivalently,
\begin{equation*} \frac { | \nabla ( {\cal A} ) | } { | N _ { k + 1} | } \geq \frac { | {\cal A} | } { | N _ { k } | } \end{equation*}
for all $A \subseteq N _ { k }$, $k = 0 , \ldots , r ( P ) - 1$, where $\nabla ( \mathcal{A} ) : = \{ q \in N _ { k + 1} : q > p \ \text { for some } p \in \mathcal{A} \}$. This equivalent property is called the normalized matching property of $P$.
Symmetric chain orders, i.e. ranked posets $P$ which can be decomposed into chains of the form $( p _ { 0 } < \ldots < p _ { h } )$ where $r ( p _ { i } ) = r ( p _ { 0 } ) + i$, $i = 0 , \ldots , h$, and $r ( p _ { 0 } ) + r ( p _ { h } ) = r ( P )$.
Peck posets, i.e. ranked posets $P$ such that $| N _ { k } | = | N _ { r \langle P \rangle -k } |$ for all $k$ and there is a linear operator $\tilde { \nabla }$ on the vector space having the basis $\{ \tilde{p} : p \in P \}$ with the following properties:
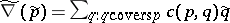 with some numbers $c ( p , q )$,
with some numbers $c ( p , q )$,
the subspace generated by $\{ \tilde { p } : p \in N _ { i } \}$ is mapped via $\widetilde { \nabla } ^ { j - i }$ to a subspace of dimension 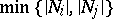 for all $0 \leq i < j \leq r ( P )$. If $P$ and $Q$ are posets from one class, then also the direct product $P \times Q$ (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: $| N _ { k } | ^ { 2 } \geq | N _ { k - 1} | | N _ { k + 1}|$ for all $k$ (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
for all $0 \leq i < j \leq r ( P )$. If $P$ and $Q$ are posets from one class, then also the direct product $P \times Q$ (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: $| N _ { k } | ^ { 2 } \geq | N _ { k - 1} | | N _ { k + 1}|$ for all $k$ (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
Every LYM poset with the symmetry and unimodality property $| N _ { 0 } | = | N _ { r(P) } | \leq | N _ { 1 } | = | N _ { r ( P ) - 1} | \leq \dots$ is a symmetric chain order and every symmetric chain order is a Peck poset.
Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an $n$-dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an $n$-dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if $n$ is sufficiently large.
Details can be found in [a1].
References
| [a1] | K. Engel, "Sperner theory" , Cambridge Univ. Press (1997) |
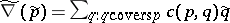 with some numbers $c ( p , q )$,
with some numbers $c ( p , q )$,
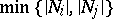 for all $0 \leq i < j \leq r ( P )$. If $P$ and $Q$ are posets from one class, then also the direct product $P \times Q$ (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: $| N _ { k } | ^ { 2 } \geq | N _ { k - 1} | | N _ { k + 1}|$ for all $k$ (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
for all $0 \leq i < j \leq r ( P )$. If $P$ and $Q$ are posets from one class, then also the direct product $P \times Q$ (ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: $| N _ { k } | ^ { 2 } \geq | N _ { k - 1} | | N _ { k + 1}|$ for all $k$ (so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.