Witch of Agnesi

versiera

A plane curve, given in the Cartesian orthogonal coordinate system by the equation

$$y(a^2+x^2)=a^3,\quad a>0.$$

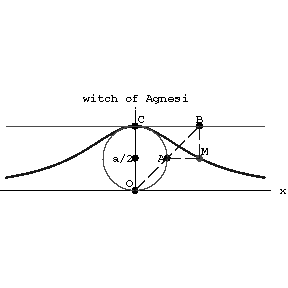
Figure: w098050a

If $a$ is the diameter of a circle with centre at the point $(0,a/2)$, $OA$ is a secant, $CB$ and $AM$ are parallel to the $x$-axis, and $BM$ is parallel to the $y$-axis (see Fig.), then the witch of Agnesi is the locus of the points $M$. If the centre of the generating circle and the tangent $CB$ are shifted along the $y$-axis, the curve thus obtained is called Newton's aguinea and is a generalization of the witch of Agnesi. The curve is named after M. Agnesi (1748), who studied it.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)

References

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)