Difference between revisions of "Semicontinuous function"
m |
m (moved Semi-continuous function to Semicontinuous function over redirect: More common terminology) |
(No difference)
| |
Revision as of 18:39, 12 August 2012
An extended real-valued function 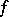 , defined on a complete metric space
, defined on a complete metric space 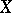 , is said to be lower (upper) semi-continuous at a point
, is said to be lower (upper) semi-continuous at a point 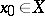 if
if
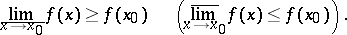 |
The function 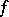 is said to be lower (upper) semi-continuous on
is said to be lower (upper) semi-continuous on 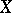 if it is lower (upper) semi-continuous at all points
if it is lower (upper) semi-continuous at all points 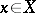 . The limit of a monotone increasing (decreasing) sequence of functions which are lower (upper) semi-continuous at a point
. The limit of a monotone increasing (decreasing) sequence of functions which are lower (upper) semi-continuous at a point 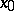 is again lower (upper) semi-continuous at
is again lower (upper) semi-continuous at 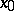 . If
. If  and
and  are, respectively, lower and upper semi-continuous on
are, respectively, lower and upper semi-continuous on 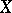 and for all
and for all  it is true that
it is true that 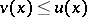 ,
, 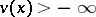 ,
, 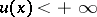 , then there exists a continuous function
, then there exists a continuous function 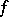 on
on 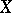 such that
such that 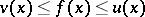 for all
for all 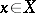 . If
. If 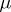 is a non-negative regular Borel measure on
is a non-negative regular Borel measure on 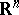 , then for any
, then for any 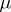 -measurable function
-measurable function 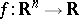 there exist two monotone sequences of functions
there exist two monotone sequences of functions 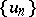 and
and 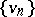 satisfying the conditions: 1)
satisfying the conditions: 1) 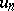 is lower semi-continuous,
is lower semi-continuous, 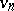 is upper semi-continuous; 2) every
is upper semi-continuous; 2) every  is bounded below, every
is bounded below, every 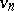 is bounded above; 3)
is bounded above; 3) 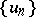 is a decreasing sequence and
is a decreasing sequence and 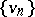 is an increasing sequence; 4) for all
is an increasing sequence; 4) for all  ,
,
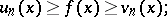 |
5) 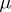 -almost everywhere,
-almost everywhere,
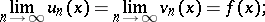 |
and 6) if 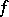 is
is 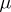 -summable over
-summable over 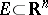 ,
, 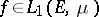 , then
, then 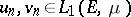 and
and
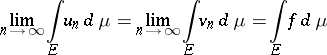 |
(the Vitali–Carathéodory theorem).
References
| [1] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
| [2] | S. Saks, "Theory of the integral" , Hafner (1937) (Translated from French) |
Comments
The expressions lower semi-continuous and upper semi-continuous are often abbreviated to l.s.c. and u.s.c.. The notions of l.s.c. and u.s.c. function can be defined on any topological space 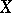 . The superior (respectively, inferior) envelope of any family of continuous functions is l.s.c. (u.s.c.), and the converse is true whenever
. The superior (respectively, inferior) envelope of any family of continuous functions is l.s.c. (u.s.c.), and the converse is true whenever 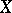 is completely regular; this holds with a countable family of continuous functions if
is completely regular; this holds with a countable family of continuous functions if 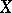 is metrizable. Consequently, a semi-continuous function on a metric space
is metrizable. Consequently, a semi-continuous function on a metric space 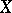 is of Baire class one (cf. Baire classes). The converse is not true.
is of Baire class one (cf. Baire classes). The converse is not true.
Let 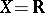 . If
. If
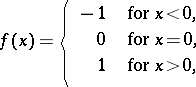 |
then 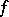 is of Baire class one, but neither lower nor upper semi-continuous. Also,
is of Baire class one, but neither lower nor upper semi-continuous. Also, 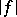 is lower semi-continuous, but
is lower semi-continuous, but
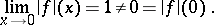 |
Note that 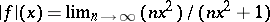 for all
for all 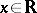 , so
, so 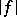 is the pointwise limit of an increasing sequence of continuous functions.
is the pointwise limit of an increasing sequence of continuous functions.
A very useful fact on semi-continuous functions is the Dini–Cartan lemma. Let 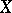 be a compact space and
be a compact space and 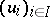 a family of l.s.c. functions such that for any finite subset
a family of l.s.c. functions such that for any finite subset 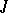 of
of 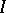 there is an
there is an 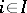 with
with 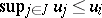 . If
. If  is an u.s.c. function such that
is an u.s.c. function such that 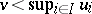 , then there is an
, then there is an 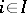 such that
such that 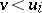 ; in particular, one has
; in particular, one has 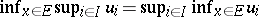 .
.
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Semicontinuous function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semicontinuous_function&oldid=27439